UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 3c.
Considere as funções:
c) . Para quais valores de e temos ? Represente graficamente a resposta.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão, foi dada uma função e temos que encontrar os valores de e para que . Mas como vamos fazer isso? 🤔
Primeiro de tudo, vamos analisar uma coisa. Foi dada uma função tridimensional, já que representa as coordenadas do eixo .
Quando determinamos , estamos determinando , ou seja, estamos “cortando” a função na altura do eixo e o que vamos encontrar, graficamente, é a intercessão de e da função , resultando em uma outra função bidimensional.
Com essas informações, podemos iniciar nosso probleminha. Bora lá!
Passo 2
Quando admitimos , podemos escrever a função assim
Isolando de um lado da igualdade, temos
Com essa informação, podemos determinar os possíveis valores de e para que a função seja igual a .
Encontramos que e pode ser qualquer número real desde que .
Uma forma mais didática de escrever isso, é
Passo 3
Podemos representar graficamente substituindo valores de na equação , o que vai nos resultar em pontos, a partir desses pontos, podemos traçar a curva que procuramos.
Vemos que em , é indefinido, portanto o gráfico será descontínuo no ponto.
Plotando os demais pontos no plano cartesiano, temos
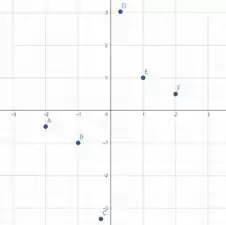
Ligando os pontos que plotamos, podemos esboçar o gráfico que representa .
Quando não temos tanta clareza sobre o gráfico que estamos trabalhando, podemos estimar mais valores para para plotar mais pontos no plano.
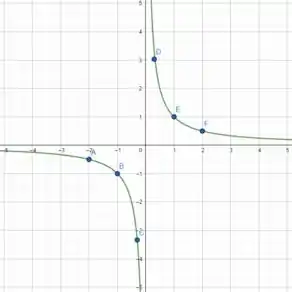
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍