UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 2d.
Esboce o gráfico das funções a seguir:
d)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Para essa questão, foi solicitado que esbocemos um gráfico de , mas você acha que podemos fazer isso? 🤔
Esboçar um gráfico é traçar, de uma forma mais material, a imagem da função.
Uma função está contida em 3 dimensões, ou seja, dependendo de um determinado ponto em e um determinado ponto em , vamos ter uma imagem em , com isso, podemos afirmar que na verdade .
Podemos comparar com uma lei muito famosa, a chamada 3° Lei de Newton ou lei da Ação e Reação. Essa lei da natureza diz que para cada ação, há uma consequência, por exemplo, se levantarmos tarde e deixar a cama desarrumada, nossa mãe vai ficar brava sendo capaz até de nos botar de castigo, não é?
Então, nossas ações são nossas variáveis e , no caso, levantar depois do horário e não arrumar a cama. Quando isso acontece, temos uma reação, ou seja, nossa variável ou , que no caso foi nossa mãe ficar brava e pôr a gente de castigo.
Entendeu? Para cada valor de e , vamos ter um (para cada ação, vamos ter uma reação)!
Passo 2
Na prática, funciona da seguinte maneira:
Temos a função que vamos esboçar o gráfico
O próximo passo é analisarmos o que esperamos de como será o gráfico.
Neste caso, como você acha que ele vai ser? Plano, ondulado, inclinado, curvo...?
Essa função vai nos perseguir durante toda a vida acadêmica, então é bastante importante ter familiaridade com funções trigonométricas.
Muito provavelmente você já viu a função cosseno em algum momento, mas se não lembra, vamos dar uma relembrada.
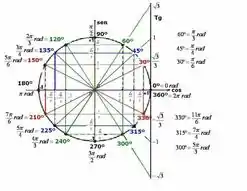
Este é o famoso circulo trigonométrico. Nele podemos ver alguns valores relacionados ao seno, cosseno e tangente.
O cosseno é o que está deitado e o seno é o que está em pé.
Quando ,
Quando ,
Quando ,
Quando ,
E quando ,
Passo 3
Substituindo estes valores em um plano , onde , temos
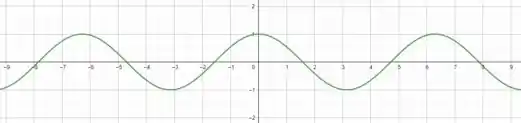
Esse é o gráfico de um cosseno em um plano de duas dimensões, mas e em três dimensões? Como fica?
Bom, não tem a variável , então se for constante, para todo o a função vai ser igual.
Neste caso, é como se estivéssemos projetando através de um feixe de laser, onde a projeção de um laser forma um ponto na parede, mas no caminho até a parede, podemos ver uma reta
Da mesma forma é no caso de , vimos sua projeção em um plano qualquer em , mas em três dimensões, o que era uma linha ondulada, vira um plano ondulado.
Veja só
Se cortássemos o plano em qualquer plano perpendicular a , vamos ter a curva que mostramos anteriormente.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Gráfico no Último Passo.