Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Funções de 2 variáveis, Curvas de Nível e Gráfico

Ver Teoria
Exercício 53123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525455565758596061

Enunciado

UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 4c.

3- Desenhe as curvas de nível f - 1 k : = x , y ∈ R 2 f x , y = k das funções de duas variáveis f a seguir para os valores de k dados:

c) f x , y = 1 2 ln ⁡ x 2 + y 2 ;   k = 0 ,   1 ,   2 ,   3 ;

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Para essa questão vamos ter que calcular as curvas de níveis da função f x , y . Ok, mas o que são curvas de níveis?

Curvas de níveis de uma função são obtidas a partir do corte na função a uma altura k do plano x y , formando uma curva correspondente à curva de nível na altura k .

Algo muito parecido com desenhos topográficos em Geografia.

Inicialmente temos uma função tridimensional, porém quando tiramos a curva de nível, obtemos uma função bidimensional, já que a variável z corresponde à altura.

Com isso podemos iniciar nossos cálculos, substituindo f x , y por k , temos

f x , y = 1 2 ln ⁡ x 2 + y 2

k = 1 2 ln ⁡ x 2 + y 2

2 k = ln ⁡ x 2 + y 2

Elevando os dois lados por e , temos

e 2 k = e ln ⁡ x 2 + y 2

e 2 k = x 2 + y 2

x 2 + y 2 = e 2 k 2

Encontramos algo muito parecido com a equação da circunferência, na verdade é exatamente igual a equação da circunferência, onde nosso raio é dado por e 2 k .

Com isso nossas curvas de níveis vão ser circunferências de raio e 2 k .

Passo 2

Agora substituímos k pelos valores que procuramos.

Para k = 0

x 2 + y 2 = e 2 0 2

x 2 + y 2 = 1 2

x 2 + y 2 = 1

Para k = 1

x 2 + y 2 = e 2 1 2

x 2 + y 2 = e 2 2

x 2 + y 2 = e 4

Para k = 2

x 2 + y 2 = e 2 2 2

x 2 + y 2 = e 4 2

x 2 + y 2 = e 8

Para k = 3

x 2 + y 2 = e 2 3 2

x 2 + y 2 = e 6 2

x 2 + y 2 = e 12

Essas equações que obtemos, são das curvas de níveis que procuramos.

Passo 3

Plotando essas curvas em k = 0 , k = 1 , k = 2 e k = 3 , temos

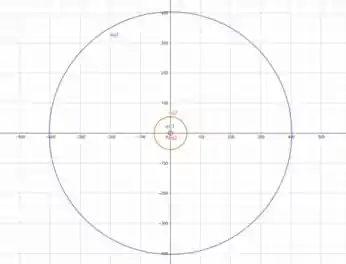
Essas são as curvas de níveis que estávamos procurando.

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

Para k = 0 , x 2 + y 2 = 1

Para k = 1 , x 2 + y 2 = e 4

Para k = 2 , x 2 + y 2 = e 8

Para k = 3 , x 2 + y 2 = e 12

Exercícios de Livros Relacionados

Desenhe as curvas de nível e esboce o gráfico. f (x , y) = 4 x^2 + y ² ²
Utilize um computador para traçar o gráfico da função usando vários domínios e pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, tr
Esboce o gráfico da função. f x , y = 4 x 2 + y 2
Utilize um computador para traçar o gráfico da função, usando vários pontos de vista e tamanhos de janela. Comente o comportamento da função no limite. O que acontece quando x e y se tornam muito gran
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha. z = x - y 1 + x 2 + y 2