UFABC. Cálculo. Lista: Funções de Várias Variáveis. Lista 1 - Domínios, Gráficos e Curvas de Nível. 2018.3. Questão: 2A.
Esboce o gráfico das funções a seguir:
a)
Passo 1
Iae, meus queridos! Tudo certinho?
Essa questão vai ser bem rapidinha.
Nosso objetivo nessa questão é esboçar o gráfico da função dada.
Neste caso, a função é
Em uma função o resultado estará na 3° dimensão, ou seja, da dimensão , logo
Na nossa função, vemos que independente de e , o valor será sempre o mesmo, assim concluímos que o gráfico de será um plano paralelo ao plano .
Por fim se , logo , ou seja, o plano cortará o eixo quando
Passo 2
Com essas conclusões que tomamos, podemos esboçar o gráfico de .
Se tratando de um plano paralelo ao plano e cortando o eixo quando , temos:
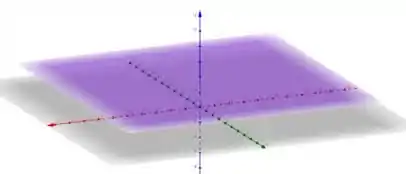
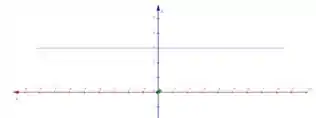
Nesta última imagem, vemos o gráfico quando
É isso! Entendeu tudo? Responde Aí! 😎👍
Resposta
Exercícios de Livros Relacionados
Desenhe as curvas de nível e esboce o gráfico. f (x , y) = 4 x^2 + y ² ²
Utilize um computador para traçar o gráfico da função usando vários domínios e pontos de vista. Imprima a que, em sua opinião, oferece a melhor visão. Se seu programa também produz curvas de nível, tr
Esboce o gráfico da função. f x , y = 4 x 2 + y 2
Utilize um computador para traçar o gráfico da função, usando vários pontos de vista e tamanhos de janela. Comente o comportamento da função no limite. O que acontece quando x e y se tornam muito gran
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha. z = x - y 1 + x 2 + y 2