UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 10.
Na Figura 3 são mostradas curvas de nível para a função . Use-as para estimar o valor de e . O que você pode dizer sobre a forma do gráfico de ?
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Para essa questão, foi dada algumas curvas de níveis de e com base nelas, temos q estimar alguns valores e fazer uma análise sobre o comportamento de .
As curvas de níveis que foram dadas, são
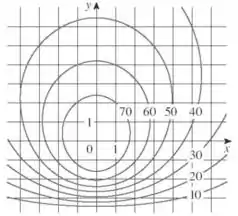
Temos que estimar os valores da função nos pontos e .
Passo 2
O ponto
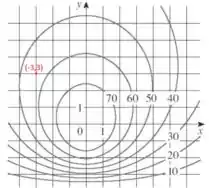
Para este ponto, vemos que ele está localizado entre as curvas dos níveis e , logo, muito provavelmente o nível que contém o ponto também esteja entre e . Ou seja
O ponto
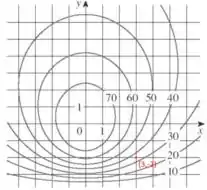
Vemos que este ponto está contido entre os níveis e da função e, também, provavelmente o nível que contém este ponto também deve estar entre estes níveis. Ou seja
Passo 3
Analisando as curvas de níveis, vemos que a função parece ser uma espécie de cone elíptico, algo como
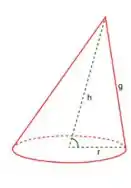
Podemos chegar nessa conclusão pois quanto menor o nível de sua curva, maior é a área inscrita na curva e conforme os níveis aumentam, as elipses vão ficando menores.
Graficamente isso representa um solido que é grosso na base e vai afinando conforme os níveis vão aumentando.
Perceba também que nosso cone é levemente inclinado, já que o centro da elipse do nível superior é deslocado para o sentido negativo de , assim como na imagem.
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
