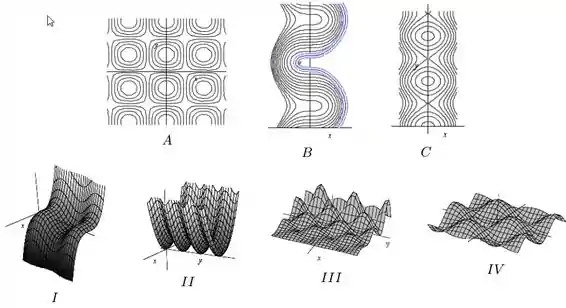
Os mapas de contorno abaixo (figuras , e ) correspondem a que gráficos (figura , , ou )?
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
Passo 1
Mano, esse tipo de questão não tem jeito, fica até difícil explicar. A única coisa a se fazer é tentar visualizar como são os cortes horizontais da superfície e comparar com as alternativas.
Passo 2
A curva é aquela que cada corte vai resultar em vários círculos iguais, que é a da figura .
Passo 3
O mapa de contorno visualizando os cortes vamos ver tipo uma ondinha com a “perna” na parte positiva do eixo . Sei lá, não tem muito o que dizer...
Enfim, não confunda com a alternativa , o gráfico certo é o .
Passo 4
O mapa se fizermos os cortes vamos ver tipo uma ondinha com parecido com a anterior mas ela é simétrica, que é o gráfico .
Repare que o gráfico lembra vários paraboloides, e de fato as bolinhas do mapa de contorno lembram as curvas de nível de um paraboloide.
Resposta
Alternativa (a)