UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 3b.
Considere as funções:
b) . Para quais valores de e temos ? Represente graficamente a resposta.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Para essa questão, foi pedido que encontremos os valores de e para que seja igual a . Mas como vamos resolver isso?
Quando temos uma função , temos uma função tridimensional, onde representa a coordenada dos eixos coordenados.
Dizer que , é dizer que , ou seja, estamos traçando um plano perpendicular ao eixo neste ponto.
Com isso, o que era uma função tridimensional, agora será uma função bidimensional. Logo a representação que vamos fazer será em duas dimensões.
Com essas ideias, podemos iniciar os cálculos para resolver nosso probleminha. Bora lá!
Passo 2
Lembrando lá de equações potenciais e de algumas propriedades de potência, todo número elevado a é igual a .
Então podemos escrever a função como
Se todo número elevado a é , .
Com este valor podemos aplicar a ideia de igualdade de equações, tal que
Comparando a potência dos , tiramos que
ou
A partir daí, podemos afirmar que para que , e pode ser qualquer numero real, desde que . Ou de forma mais didática, podemos escrever a mesma coisa como
Passo 3
Como podemos representar isso graficamente?
Um método muito interessante quando temos uma função esteticamente simples assim, é substituir a variável por um número e observar o resultado em . Por exemplo
Plotando os pontos que encontramos , temos
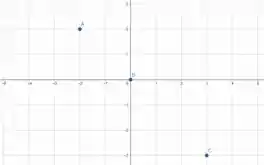
Como ou se tratam de uma reta, podemos traçar uma reta ligando os pontos que plotamos, com isso, vamos obter graficamente os valores de e que satisfazem a igualdade de
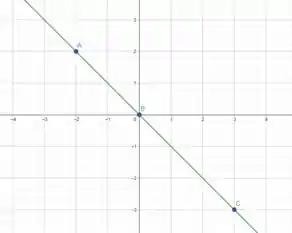
É isso! Essa resolução te ajudou? Responde Aí! ✌