Esboce o gráfico das funções a seguir:
f)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Para essa questão, foi solicitado que esbocemos um gráfico de , mas você acha que podemos fazer isso? 🤔
Esboçar um gráfico é traçar, de uma forma mais material, a imagem da função.
Uma função está contida em três dimensões, ou seja, dependendo de um determinado ponto em e um determinado ponto em , vamos ter uma imagem em , com isso, podemos afirmar que na verdade .
Podemos comparar com uma lei muito famosa, a chamada 3° Lei de Newton ou lei da Ação e Reação. Essa lei da natureza diz que para cada ação, há uma consequência, por exemplo, se gastarmos todo nosso dinheiro antes do fim do mês, muito provavelmente vamos atrasar uma conta ou sofrer por um gasto não previsto, não é?
Então, nossas ações são nossas variáveis e , no caso, gastar todo o dinheiro. Quando isso acontece, temos uma reação, ou seja, nossa variável ou , que no caso foi ficar no negativo.
Entendeu? Para cada valor de e , vamos ter um (para cada ação, vamos ter uma reação)!
Passo 2
Na prática, funciona da seguinte maneira:
Temos a função que vamos esboçar o gráfico
O próximo passo é analisarmos o que esperamos de como será o gráfico.
Neste caso, como você acha que ele vai ser? Plano, ondulado, inclinado, curvo...?
Analisando a função vemos que ela aparece com a equação da circunferência, onde . Podemos imaginar, então que nossa função terá alguma relação com a equação da circunferência.
Neste caso, a forma mais fácil de construir o gráfico da função, é construir a partir das curvas de níveis da função. Algo muito semelhante com os desenhos topográficos de geografia.
Este método consiste em ao invés de estimar valores para e , vamos estimar valores para .
Usamos este método quando temos uma função já conhecida, como neste caso.
Passo 3
O método de tabelar valores estimados, continua sendo elaborado, mas estimando o valor de
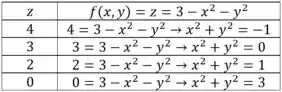
No plano , encontramos , como não existe circunferência de numero negativo, podemos descartar este nível.
No plano , encontramos , ou seja, um ponto.
Nos planos e , encontramos e respectivamente, ou seja, uma circunferência de raio 1 e outra circunferência de raio .
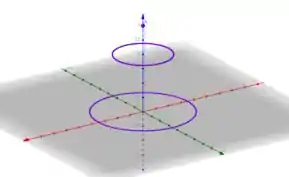
Se plotarmos esses gráficos em seu respectivo plano de , temos
Por fim, ligamos as curvas que plotamos para obter o plano relativo à função
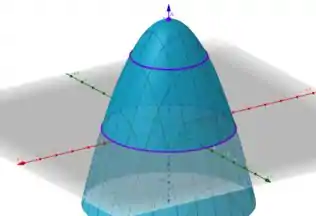
Vemos que possui imagem em valores menores ou igual a , já que para valores maiores, não é possível ser obtidos.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta
Gráfico no último passo.