UFABC. Cálculo. Funções de Várias Variáveis. Lista 1. Questão 8c.
8- Seja .
c) Faça um esboço do gráfico de .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
O probleminha nos pediu pra esboçar o gráfico de , mas par ser sincero, dificilmente vamos conseguir imaginar como é o gráfico de uma função só de olharmos para ela, então temos que dispor de alguns artifícios pra nos ajudar nessa tarefa.
Existe um método de tabelamento dos valores de entrada para plotarmos pontos que fazem parte da superfície da função, mas este método não é muito bom para funções tridimensionais, como nesse caso, já que teríamos que plotar muuuitos pontos para começarmos a imaginar o gráfico.
Para funções tridimensionais, uma boa forma de construir um gráfico é calcular algumas curvas de níveis e intercessões com planos. Estas intercessões e curvas de níveis vão resultar em funções bidimensionais, com essas funções conseguimos esboça-las em sendo contida no plano em que foi calculada.
Passo 2
Vamos calcular a intercessão entre e os planos , , , , e .
Antes vamos fazer um ajuste na função e trocar por
Elevando os dois lados ao quadrado para eliminar a raiz, temos
Observe que a raiz inicial é positiva, então só pode assumir valores positivos.
Para , temos
Para , temos
Para , temos
Para , temos
Para , temos
Por fim, para , temos
Passo 3
Nos resta plotar estas curvas contidas em seus planos, por exemplo, vamos plotar no plano , no plano e assim por diante. Isso vai resultar em algo parecido como uma estrutura da superfície, veja só
Quanto mais curvas de níveis fizermos, mais fácil será para construirmos o gráfico da função.
Ligando as curvas, vamos ter o gráfico de
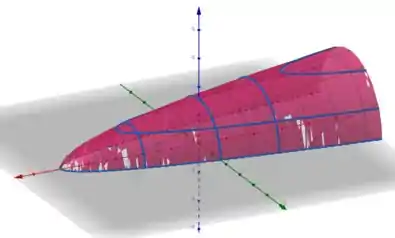
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
Gráfico descrito no passo-a-passo.