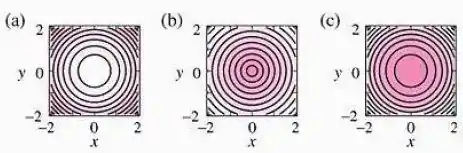
Em cada parte, associe o mapa de contorno com uma das funções
por inspeção, e explique seu raciocínio. Quanto maior o valor de , mais clara fica a cor no mapa de contorno e os contornos correspondem a valores igualmente espaçados de .
Passo 1
Pra gente poder relacionar as funções com os mapas de contorno, precisamos ter uma noção de como é o gráfico de cada uma delas. Então vamos começar fazendo isso, ok?
Primeira função :
Fazendo :
Elevando tudo ao quadrado:
Opa, isso é a equação de um cone circular!
Mas como nosso é uma raiz quadrada, devemos ter . Então na verdade a superfície é somente a metade superior de um cone circular.
Passo 2
Agora vamos ver como são as curvas de nível do gráfico dessa função.
Fazemos
Que nada mais é que uma circunferência centrada em e de raio .
Ou seja, as curvas de nível de um cone circular são circunferências (que surpresa!). Mas no caso isso não vai ajudar porque os 3 mapas de contorno só têm circunferências.
Então já sabemos que pras outras funções também nem adianta identificar a natureza das curvas de nível, todas vão ser circunferências.
Passo 3
Então agora vamos ter que analisar a cor dos mapas de contorno. Ele disse que quanto maior o valor de , mais clara a cor.
O ponto mais baixo, ou vértice, do nosso pedaço de cone é a origem! Lembra que vimos que ? Portanto na origem a cor do mapa deve ser mais escura que no resto todo dele.
Esse rosa aí da figura é clarinho, mas bom, ele é mais escuro que o branco né? Então o mapa de contorno que queremos tem que ter o centro rosa, o mais escuro possível.
Olhando as opções que ele deu já podemos eliminar a alternativa (a), que tem o centro branco.
Passo 4
Mesmo assim, tendo bem em mente como é o cone, já podemos determinar qual é o mapa de contorno certo:
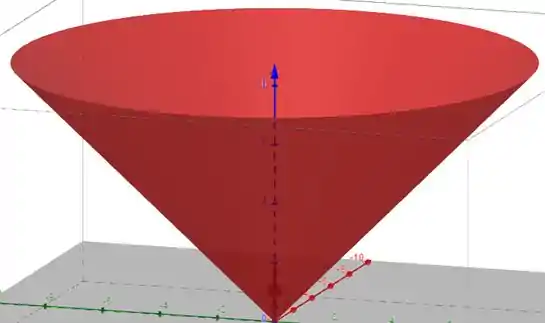
Repare que ele sobe retinho (ele faz um ângulo de com o plano ), isso é um indício que as suas curvas de nível são igualmente espaçadas uma da outra. Assim a alternativa (b) estaria certa.
Mas isso é mais uma intuição que dá pra ter, é claro que podemos confirmar isso olhando as outras funções.
Passo 5
Então vamos dar uma olhada nessas funções. Temos
que é uma clássica! Inclusive provavelmente você já se deparou com ela em algum momento.
Fazendo
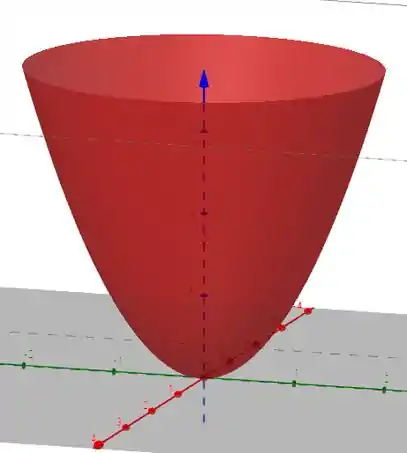
obtemos a equação de um paraboloide circular. É aquele que cortando na vertical obtemos parábolas e na horizontal circunferências.
Ele é assim:
Passo 6
Assim como pro cone, o vértice do paraboloide é a origem. Portanto, o centro do seu mapa de contorno também tem que estar em rosa.
Então, da mesma forma, podemos eliminar a alternativa (a).
Ou seja, dentre as alternativas (b) e (c), uma é do cone e a outra do paraboloide. E a alternativa (a) é da outra função (depois vamos verificar).
Pensando nos gráficos dessas superfícies e olhando as alternativas já dá pra determinar qual é qual!
O paraboloide é mais gordinho perto da origem, ele demora mais a crescer: por isso suas primeiras curvas de nível são mais espaçadas. Depois ele cresce bem rápido, o que faz suas curvas de nível serem mais próximas.
Por isso a alternativa (c) parece bem apropriada pra ele.
Passo 7
Mas vamos ver isso com mais calma, pra não ficar nenhuma dúvida :)
Pra visualizar melhor essas curvas de nível, podemos ver como é a interseção dessas superfícies com o plano (poderia ser também), zerando a variável .
Passo 8
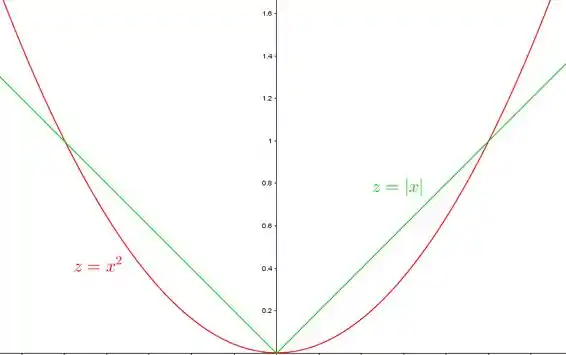
Então no plano o que observamos é isso aqui:
Passo 9
Ou seja, no cone andamos sempre na mesma velocidade, o que faz as curvas de nível serem igualmente espaçadas pra valores igualmente espaçados de .
E no outro estamos seguindo uma função quadrática: as curvas de nível vão ficar cada vez mais próximas pra valores igualmente espaçados de .
Passo 10
Vou até dar uma incrementada na figura pra ficar mais claro. Pra obter as curvas de nível nós cortamos as superfícies com planos horizontais certo?
Então vamos fazer isso. O detalhe é que no plano vamos observar não planos, mas retas:
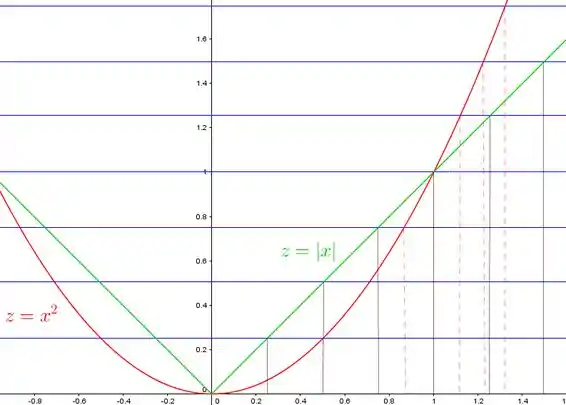
Repare como a distância entre as “curvas de nível” se mantém constante pra reta , enquanto pra parábola elas vão se aproximando cada vez mais.
Realmente podemos concluir que a alternativa (b) corresponde à função , enquanto a alternativa (c) corresponde a .
Passo 11
Por eliminação, resta a alternativa (a) e a função .
Vejamos que superfície é o gráfico dessa função:
Se você estiver manjando bem do assunto, vai perceber que é também um paraboloide circular, mas virado pra baixo.
Então na verdade o seu mapa de contorno vai ser bem parecido com o do outro paraboloide, que é o da alternativa (c). E de fato as alternativas (a) e (c) se parecem.
A diferença é que como dessa vez o paraboloide está virado pra baixo, seu vértice é o seu ponto mais alto. Assim o centro do seu mapa de contorno tem que estar mais claro.
E realmente o centro do mapa de contorno da alternativa (a) está branquinho como neve.
Então ótimo, está tudo fazendo sentido! :)