UFU, Sem Campus, Cálculo 3, Listas de Cálculo 3 - Profª Lúcia - Lista de Integral de Linha - 2023.1, Questão 1b
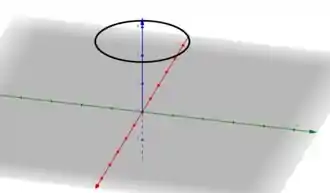
1. Esboce a imagem da curva , indicando o seu sentido de percurso, sendo:
b) , .
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema foi dada uma curva parametrizada e nosso objetivo é esboçar seu gráfico e indicar o sentido do seu percurso.
Tem ideia de como fazer isso? 🤔
Para verificar como o gráfico de se comporta, podemos “desparametrizar” a função ou analisar o comportamento da função parametrizada...
Sacou? Bora começar! 😁
Passo 2
Se a função parametrizada é dada por
Podemos imaginar que a função foi parametrizada como por coordenadas polares em que , e , ou seja
A partir dessas informações vamos que a função se trata de uma circunferência de raio 3 contida em .
Esboçando essa curva, temos
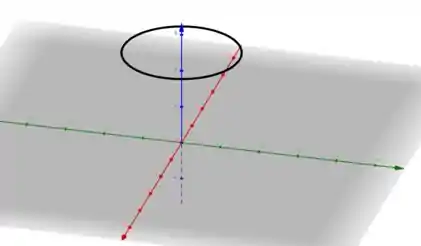
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
