Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Parametrização de Curvas

Ver Teoria
Exercício 501234567891011121314151617181920212223242526272829303132333435363738394041424344454647484951525354555657585960

Enunciado

UFPE, Sem Campus, Cálculo 3, Listas de Cálculo 3 - UFPE - Integrais de Linha, Questão 9a

Calcule ∫ C P   d x + Q   d y + R   d z , onde:

a) F → = P ,   Q ,   R = ( y ,   z ,   x ) e C é a interseção de x + y = 2 e x 2 + y 2 + z 2 = 2 x + 2 y , percorrida no sentido anti-horário quando vista da origem.

Passo 1

Fala, galera! Vamos resolver essa questão!

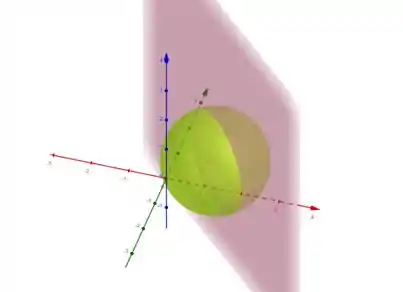
O enunciado nos deu uma integral de linha pra ser calculada na região de interseção entre a esfera e o plano, nessa região aqui:

Dadas as componentes do vetor F → = P ,   Q ,   R = ( y ,   z ,   x ) , podemos montar nossa integral ∫ C P   d x + Q   d y + R   d z da seguinte forma:

∫ C y   d x + z   d y + x   d z

Só falta a gente definir a região a C , analisando a interseção das curvas pra definir uma parametrização e encontrar nossos intervalos de integração.

Vamos lá!

Passo 2

Como nossa região de integração é a interseção entre as curvas x + y = 2 e x 2 + y 2 + z 2 = 2 x + 2 y , vamos ter:

x 2 + y 2 + z 2 = 2 ( x + y )

Da equação do plano, podemos definir:

x + y = 2 → y = 2 - x

Substituindo na primeira igualdade:

x 2 + ( 2 - x ) 2 + z 2 = 2 ( 2 )

2 x 2 - 4 x + 4 + z 2 = 4

Dividindo todo mundo por 2 :

x 2 - 2 x + 2 + z 2 2 = 2

Fatorando a equação:

x - 1 2 + z 2 2 = 1

Obtivemos nossa interseção. Dessa forma, considerando a projeção no plano O x z com a orientação dada, temos a parametrização:

x t = 1 + cos ⁡ t

y t = - 2 sin ⁡ t

0 ≤ t ≤ 2 π

Passo 3

Agora podemos montar nossa integral:

∫ C y   d x + z   d y + x   d z

∫ 0 2 π ( 1 - cos ⁡ t ) sin ⁡ t d t + ∫ 0 2 π - 2 sin ⁡ t sin ⁡ t d t ∫ 0 2 π ( 1 + cos ⁡ t ) ( - 2 cos ⁡ t ) d t

Resolvendo os produtos:

∫ 0 2 π sin ⁡ t d t - ∫ 0 2 π - cos ⁡ t sin ⁡ t d t + ∫ 0 2 π - 2 sin 2 ⁡ t d t - 2 ∫ 0 2 π cos ⁡ t d t - 2 ∫ 0 2 π cos 2 ⁡ t d t

Calculando as integrais:

- cos ⁡ t + sin 2 ⁡ t 2 - 2 t 2 - sin ⁡ 2 t 4 - 2 sin ⁡ t - 2 t 2 + sin ⁡ 2 t 4 0 2 π

Aplicando os intervalos de integração, obtemos:

- cos ⁡ 2 π + sin 2 ⁡ 2 π 2 - 2 2 π 2 - sin ⁡ 2 2 π 4 - 2 sin ⁡ 2 π - 2 2 π 2 + sin ⁡ 2 2 π 4 - - cos ⁡ 0 + sin 2 ⁡ 0 2 - 2 0 2 - sin ⁡ 2 ( 0 ) 4 - 2 sin ⁡ 0 - 2 0 2 + sin ⁡ 2 ( 0 ) 4

= - 2 π 2

Prontinho, galera! Até a próxima! 😉

Resposta

- 2 π 2

Exercícios de Livros Relacionados

Como se calcula a área de uma superfície parametrizada no espa-ço? E de uma superfície implicitamente definida F(x, y, z) = 0?E da superfície que é o gráfico de z = ƒ(x, y)? Dê exemplos
Calcule 1C F ∙ T ds para o campo vetorial F = x2i – yj ao longoda curva x = y2 de (4, 2) a (1, –1).
Calcule int_C x y d x + ( x + y ) d y ao longo da curva y = x^2 de ( - 1,1 ) a ( 2,4 )
O que são integrais de linha? Como elas são calculadas? Dêexemplos
Calcule as integrais nos Exercícios 9 e 10.10. ∫ y 2d x + x 2d x C é a circunferência x 2 + y 2 = 4 .