Parametrize a curva , fronteira do triângulo de vértices , e , orientada no sentido anti-horário.
Dica: Aqui é preciso parametrizar cada um dos lados do triângulo de forma independente, afinal, cada um deles é um segmento de uma reta diferente.
Passo 1
Como já diz a nossa dica, vamos precisar descobrir a equação de cada uma das retas pra poder parametrizar a curva inteira.
Lembrando que a parametrização nada mais é do que definir os valores de de forma independente e em função de um único parâmetro (pode chamar de uma variável também, é o mesmo significado de parâmetro)
Antes de mais nada, vamos esboçar esse triângulo
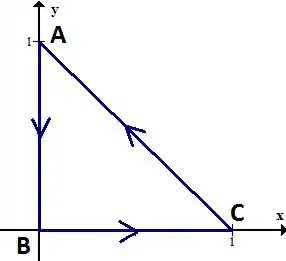
Beleza, precisamos então, para cada um dos lados do triângulo, encontrar o vetor direção e depois parametrizar o segmento de reta tomando cuidado com o sentido que escolhemos.
Tendo o vetor direção , onde e indicam a direção do vetor, e sabendo o ponto inicial , sabemos que a parametrização do segmente vai ser
Depois escolhemos ou para determinar os limites de , vamos lá?
Passo 2
Vamos começar pela reta que se encontra no eixo , vamos chama-la de . Ela é o segmento de reta que liga a , certo? Seu vetor direção
É importante lembrar que , que seria o vetor no outro sentido, tome cuidado com isso!
Beleza, nessa reta aqui, já temos dois pontos e , podemos escolher qualquer um deles como , o que vai mudar vão ser os limites de . Aqui vou fazer os dois casos só pra você ver como fica, nas próximas retas vamos sempre escolher apenas um.
Para o ponto a parametrização fica
Ué? pode ser igual a zero?! Pode sim! O que isso quer dizer é que, para qualquer valor de , a coordenada da reta vai sempre ser zero. Se você olhar pro esboço dá pra perceber que isso é verdade.
E quais os limites de nesse caso? Vamos ver isso por , que vai de a
E se escolhêssemos o outro ponto dessa reta pra fazer a parametrização? Olha só como fica!
Sendo que vai de a também, com isso
Ambas parametrizações estão corretas!
Passo 3
Vamos para o próximo seguimento de reta, chamaremos de que liga a . Para encontramos o vetor direção é só fazer o ponto final menos o inicial, certo?
Escolhendo o ponto para parametrizar essa reta ficamos com
De novo um termo é igual a zero e, de novo, isso não é problema! Veja que realmente sempre é zero nessa reta, tranquilo? Vamos ver os limites de agora.
Sabemos que vai de até , portanto
Passo 4
Vamos para o último segmento de reta , aquele que liga a . Novamente vamos encontrar o vetor direção pela diferença entre os pontos final e inicial
Escolhendo o ponto para parametrizar a reta, ficamos com
Para determinar os limites de , sabemos que começa valendo zero no ponto e termina valendo no ponto , portanto
Veja que, pela parametrização de
Portanto, de fato essa parametrização leva até .
Passo 5
Pronto! Agora só juntando tudo pra ficar bonito
Onde