USP, Sem Campus, Cálculo 3, lista 3 - 2022.1, Questão 27.
27. Seja a parte do plano limitada pelo cilindro . Uma parametrização da superfície é
a) , , com e .
b) , , , com e .
c) , , com e .
d) , , com e
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema queremos obter uma parametrização para a superfície que é dada pelo plano limitada pelo cilindro .
Como vamos fazer isso? 🤔
A parametrização de uma curva envolve expressar cada coordenada da curva como uma função de um ou dois parâmetros. Isso significa que podemos descrever a curva como um conjunto de equações paramétricas, onde cada equação dá a coordenada da curva em relação a um parâmetro específico.
Quando parametrizamos uma curva, buscamos facilitar o entendimento sob aquela curva ou área em específico.
Sacou? 😉
Passo 2
Vamos começar plotando nossa superfície .
Ela faz parte do plano e é limitada pelo cilindro
Ou seja
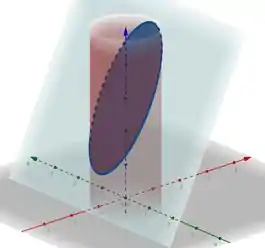
A esquerda vemos o plano e o cilindro formando nossa superfície e a direita vemos a superfície.
Se visualizarmos essa região de cima, vemos que a figura que é projetada no plano é uma circunferência de raio . Se lembrarmos da parametrização para coordenadas polares, podemos aplicar algo muito parecido aqui.
Se fizermos e , conseguimos descrever toda a projeção de no plano .
Porém ainda falta projetarmos a altura . Como e , então
Portanto, a parametrização de no domínio de é
Com sendo o raio da projeção em variando de a e o ângulo que a projeção faz com a origem, no caso de a
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
a) , , com e