UFU, Sem Campus, Cálculo 3, Listas de Cálculo 3 - Profª Lúcia - Lista de Integral de Linha - 2023.1, Questão 1a
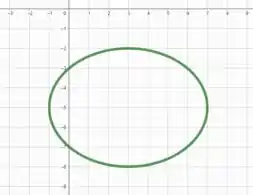
1. Esboce a imagem da curva , indicando o seu sentido de percurso, sendo:
a) , .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema foi dada uma curva parametrizada e nosso objetivo é esboçar seu gráfico e indicar o sentido do seu percurso.
Tem ideia de como fazer isso? 🤔
Para verificar como o gráfico de se comporta, podemos “desparametrizar” a função ou analisar o comportamento da função parametrizada...
Sacou? Bora começar! 😁
Passo 2
Se a função parametrizada é dada por
Podemos imaginar que a função foi parametrizada como por coordenadas polares em que e , ou seja
Como os termos que multiplicam e são diferentes, podemos determinar que a figura formada se trata de uma elipse centrada em com e ...
Perceba que substituindo e na equação, vemos que a igualdade será satisfeita...
Portanto o gráfico de será dado por
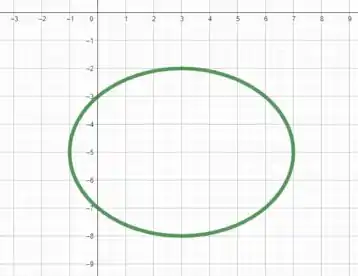
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
