UFU, Sem Campus, Cálculo 3, Listas de Cálculo 3 - Profª Lúcia - Lista de Integral de Linha - 2023.1, Questão 1c
1. Esboce a imagem da curva , indicando o seu sentido de percurso, sendo:
c) , .
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema foi dada uma curva parametrizada e nosso objetivo é esboçar seu gráfico e indicar o sentido do seu percurso.
Tem ideia de como fazer isso? 🤔
Para verificar como o gráfico de se comporta, podemos “desparametrizar” a função ou analisar o comportamento da função parametrizada...
Sacou? Bora começar! 😉
Passo 2
Se a função parametrizada é dada por
Podemos imaginar que a função foi parametrizada como por coordenadas polares em que
Como , temos que
Mas se , então...
Portanto, o gráfico da nossa curva é dado por .
Mas como temos que se ...
E se
Esboçando essa curva sabendo o intervalo de , temos
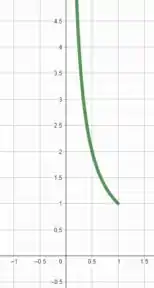
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
