Parametrize a curva dada pela interseção do cilindro com o plano
Passo 1
Bom, galera, interseção de superfícies aqui, né? Vamos esboçar tudo aqui antes de mais nada pra visualizar melhor a questão
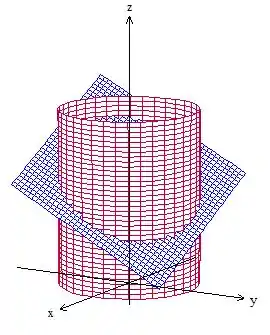
A curva é essa aqui
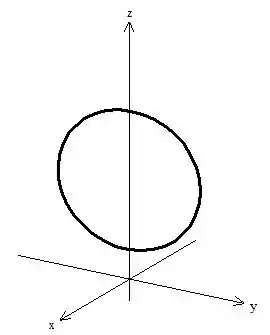
Para parametrizar isso vamos ter que analisar as equações das superfícies
Passo 2
Vamos analisar essa primeira equação do cilindro ali de cima, podemos parametrizar pela equação fundamental da trigonometria
Bem simples até, né? Foi porque escolhemos essa equação, que é uma daquelas clássicas, primeiro! Sempre comece pela equação que é fácil de ser parametrizada, beleza?
Passo 3
Vamos continuar aqui então. Já temos e parametrizados, certo? Conseguimos encontrar os parâmetros de pela equação do plano!
Substituindo os valores de e
E pronto, agora só pra organizar, nossa curva pode ser escrita de uma forma única como