UFPE, Sem Campus, Cálculo 3, Listas de Exercícios de Cálculo 3 - Profº Cilon Perusato - Lista 3, Questão 4a
Questão 4. Seja a superfície dada pela parte da esfera , calota esférica, que está acima do plano . Considere a função definida em uma região de que contém .
(a) Parametrize a superfície
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema nosso objetivo é parametrizar a superfície que é dada pela parte da esfera onde .
E aí, lembra como fazemos isso? 😐
Nesse caso, como já foi dito que a superfície é a parte da esfera onde , ou seja, é uma calota esférica, não precisamos inventar a roda... podemos usar a parametrização por coordenadas esférica.
Nessa parametrização, chamamos , e .
Lembra disso? 😁
Passo 2
Parametrizando a superfície em função de , e , vamos obter
A variável é relacionada ao raio da esfera e como vemos na equação da esfera vemos que .
A variável relaciona o ângulo que a superfície faz com o semieixo positivo de .
Esboçando uma seção da superfície , temos
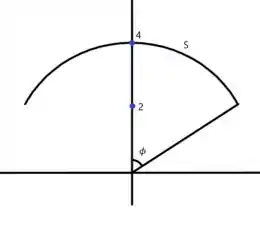
Quando , temos e para obter o valor máximo
Com isso podemos descobrir que varia de a .
Entendeu essa parte? 😐
Passo 3
Por último, temos que obter e como é o ângulo que a projeção da superfície no plano faz com o semieixo positivo de , temos que varia de a .
Portanto, podemos definir a parametrização da superfície como
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
