UFU, Sem Campus, Cálculo 3, Listas de Cálculo 3 - Profª Lúcia - Lista de Integral de Linha - 2023.1, Questão 1d
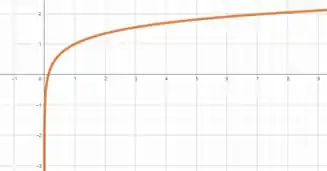
1. Esboce a imagem da curva , indicando o seu sentido de percurso, sendo:
d) , .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema foi dada uma curva parametrizada e nosso objetivo é esboçar seu gráfico e indicar o sentido do seu percurso.
Tem ideia de como fazer isso? 🤔
Para verificar como o gráfico de se comporta, podemos “desparametrizar” a função ou analisar o comportamento da função parametrizada...
Sacou? Bora começar! 😉
Passo 2
Se a função parametrizada é dada por
Podemos imaginar que a função foi parametrizada em que e
Vamos tentar isolar em para substituir em ...
Tirando nos dois lados, temos
Dessa forma se , então...
Esboçando essa curva no plano cartesiano, temos
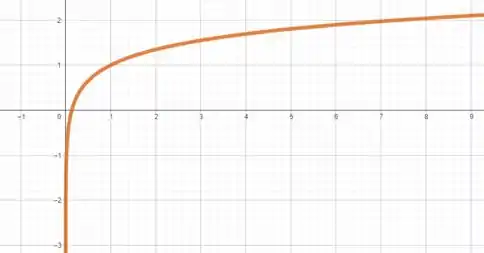
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
