(a) Identifique e faça um esboço da superfície no espaço dada por .
(b) Parametrize a curva em que é interseção das superfícies e do paraboloide hiperbólico dado por .
(c) Encontre o comprimento da curva da origem até o ponto .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

No item a) foi dada uma superfície descrita por e temos que simplesmente esboçar seu gráfico.
Já no item b) a coisa começa a ficar um pouquinho mais difícil. Temos que obter a intersecção entre e uma outra superfície dada por e com base nessa intersecção, parametrizar o vamos chamar de curva .
E no item c) temos que encontrar o comprimento de da origem do sistema até o ponto .
E aí? Parece tranquilo pra você? 👀
Vamos começar resolvendo o item a).
Bora lá!
Passo 2
Para obter o gráfico de podemos começar isolando em um lado da equação
Esse gráfico é conhecido por nós já que é muito parecido com
Como não influencia no resultado, o gráfico será o mesmo em qualquer . Plotando o gráfico de , temos
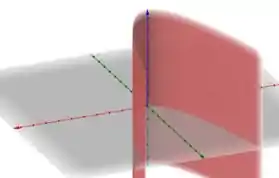
No item b) temos que parametrizar a intersecção entre e o que vai nos resultar na curva .
Lembrando que a parametrização de uma curva significa que vamos escrever tudo em função de uma única variável .
Para começar, vamos escrever uma das variáveis como para usar como referência.
Temos duas superfícies
Se usarmos , . Como , , logo
Isolando na segunda equação, temos
Substituindo e pela parametrização que fizemos, vamos obter
Logo, a parametrização da curva é dado como
Tranquilo até aqui? 😁
Passo 3
Por último, no item c) temos que calcular o comprimento da curva da origem do sistema até o ponto .
A distancia de uma curva parametrizada é dada por
é dado pelo ponto inicial da parametrização, no caso , como , vemos que .
é dado pelo ponto final da parametrização, ou seja . Se , .
Agora temos que calcular o gradiente de .
Por derivação polinomial e pela regra da cadeia, temos
Calculando o módulo desse vetor, temos
Colocando todos no mesmo denominador, temos
Com isso, calculamos a integral que vai nos resultar no comprimento de entre e .
Bacana, não é?
Passo 4
Podemos simplificar um pouquinho nossa segunda integral que pode facilitar nossa vida
Tirando as constantes para fora, temos
Escrevendo as raízes em potências
Por integração polinomial, temos
Aplicando os limites de integração, temos
Substituindo os resultados em , vamos obter
Encontramos que o comprimento da curva entre a origem do sistema até o ponto é de unidades de comprimento!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta
a) No passo 2!
b)
c)