Seja a superfície de equação . Encontre uma parametrização para a intersecção de com o plano .
Passo 1
Essa superfície é bem difícil de esboçar, galera, se você não conseguiu não tem problema. A gente vai te mostrar aqui como ela é, mas você pode fazer a questão sem esse esboço. A superfície é essa aqui
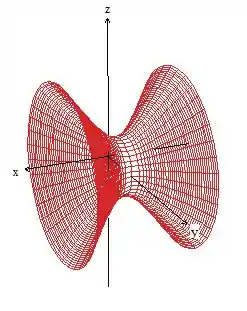
Precisamos da interseção dessa curva com o plano , o esboço é esse
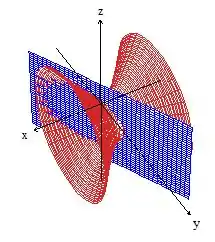
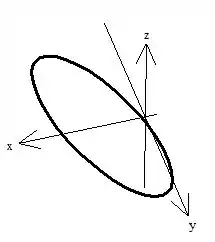
Vamos precisar analisar as duas equações pra dar um jeito de escrever tudo em função de um parâmetro só, vamos lá?
Passo 2
As equações são essas aqui
Vamos tentar isolar algum termo na segunda e substituir na primeira pra ver como fica
Tendo isolado, agora vamos substituir na primeira equação
Precisamos transformar esse termo em algo da forma
Voltando pra equação
Não podemos parametrizar ainda com a equação dessa forma, precisamos deixar o termo do lado direito da equação! Não tem problema, só dividir por nos dois lados
Passo 3
Tendo a equação dessa forma, para parametrizar é só relacionar isso com a equação fundamental que diz
Passo 4
Pronto, agora que temos a parametrização de e fica fácil achar a de , só procurar alguma equação mais fácil e substituir. A equação do plano parece mais simples, né?
Passo 5
Pronto! Só resumindo tudo aqui na resposta e ficamos com a seguinte parametrização