Cálculo Aplicado – 1ª Atividade Avaliativa – 2021.1 – Prof. Thiago de Souza Pinto
Calcule a integral de linha , onde consiste na metade superior da circunferência de a e no segmento de reta de a
Passo 1
A primeira coisa que a gente tem que se ligar é que a integral de linha do problema
pode ser escrita na forma
Com
Outra coisa que devemos fazer é uma representação do caminho . Primeiro ele começa com um pedaço de , que é um círculo de raio 2, que liga os pontos e . Para facilitar a gente vai chamar esse trecho de . Depois ele fala que tem uma reta que liga esse ponto ao ponto que a gente vai chamar de . Olha só como esse caminho fica
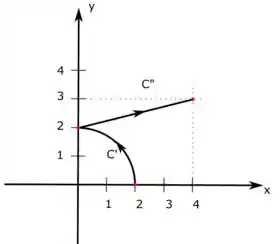
A gente observa que o caminho total é e vamos resolver esse problema calculando a integral de linha em e depois em porque temos
Passo 2
Vamos começar resolvendo a integral ao longo de
Para resolver essa integral de linha a gente tem que escrever o caminho através de uma curva parametrizada e usamos
Doideira né? Mas vem comigo que vai dar bom!
Vamos conhecer quem é quem nessa integral da direita. Como a nossa curva é um pedaço de círculo de raio , podemos usar as coordenadas polares e escrever
Dessa forma, a curva parametrizada é
Mas como que a gente diz que vamos ter um pedacinho do círculo? Olha, o nessa equação é o ângulo. Se temos só um quarto do círculo, temos que ter
E aí a gente já vê que e .
A função , usando agora o ) e fica assim ó:
Aquele que aparece na fórmula é só a derivada de em relação ao tempo
Passo 3
Usando todas essas informações em
Temos
Resolvendo o produto escalar que surge na integral
Passo 4
Ambas as integrais podem ser resolvidas usando o método da substituição simples. Olha só a primeira
Se escolhermos , temos . Os limites da integral a gente muda usando
Então temos
Da mesma forma, podemos resolver a segunda integral usando a substituição simples
Se escolhermos , temos . Os limites da integral a gente muda usando
Então temos
Passo 5
Juntando nossos resultados temos
E assim a gente calcula a integral pelo primeiro caminho
Passo 6
Agora vamos para o caminho . Como ele é uma reta, a parametrização da curva é:
Mas quem são esses ? Bem, o e o são as componentes de um vetor paralelo à reta. A gente calcula esses caras usando dois pontos da reta... Que pontos? O problema já nos dois os pontos e a gente precisa apenas fazer uma subtração entre eles
Dessa forma a gente tem
O e o são as componentes de qualquer ponto da reta. Para facilitar, vou usar o ponto então temos
Então a gente conseguiu a parametrização
Como o ponto inicial é o para chegar nele através dessa parametrização temos que ter e para o ponto (4,3) temos que ter .
A função , usando agora o ) e fica assim ó:
Aquele que aparece na fórmula é só a derivada de em relação ao tempo
Passo 7
Usando todas essas informações em
Temos
Resolvendo o produto escalar que surge nessa integral
Passo 8
Ufa!! Finalmente podemos escrever