Considere no espaço um trapézio ABCD, em que AB, BC, CD e AD são lados desse trapézio e os lados AD e BC são paralelos, como ilustrado na figura abaixo:

Seja M o ponto do segmento CD tal que . Suponha que:
E que as medidas dos ângulos e sejam iguais a . Seja um vetor não paralelo ao plano que contém o trapézio ABCD e considere a base
De . As coordenadas do vetor na base B são:
Passo 1
Falaaa, blz??? Para começarmos a pensar nessa questão vamos desenhar um pouco para nos ajudar a entender o que precisamos fazer
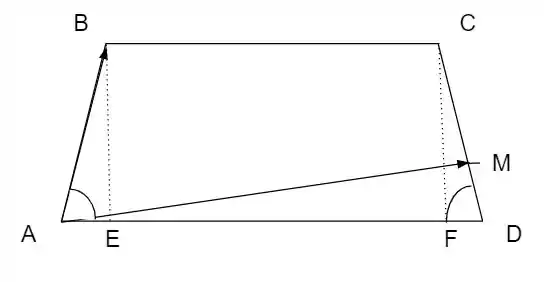
Agora, veja que queremos , mas podemos escrever como:
Veja que nosso objetivo nessa questão, portanto, é escrever esses vetores de cima em função de
Bora lá?
Passo 2
Primeiro, como , o primeiro vetor da soma já ta em função dos vetores de B, pois é um vetor de B, agora bora escrever .
Primeiro, temos que
Além disso, temos que
Ou seja, temos
E pela figura podemos escrever , mas como , temos que:
Ou seja, conseguimos escrever em função de vetores de B, agora falta só
Passo 3
Bora achar em função dos caras de B:
Para isso, basta notar que
E temos
Ou seja, temos:
Agora bora unir tudo isso na equação inicial...
Ou seja, em termos da base B, dizemos que , finalmente chegando na resposta
Resposta
Letra A