Seja fixada uma orientação no espaço . Considere as seguintes afirmações:
- Para quaisquer com não nulo, vale que é ortogonal a ;
- Se é uma base ortonormal de e se e , então ;
- Se e são bases negativas de e se e denotam as matrizes de mudança de base, então e .
Assinale a alternativa correta:
- apenas a afirmação (I) é verdadeira;
- apenas a afirmação (II) é verdadeira;
- todas as afirmações são verdadeiras;
- apenas as afirmações (I) e (II) são verdadeiras;
- apenas as afirmações (II) e (III) são verdadeiras.
Passo 1
Fala aí, meu povo! Tudo certinho por aí? Vamos analisar cada uma das três afirmações por etapas, começando com (I). Pois bem, como uma imagem vale mais do que mil palavras, vamos ilustrar rapidamente a projeção ortogonal de um vetor na direção determinada por outro:
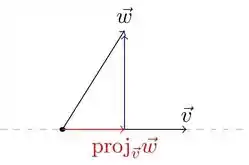
Conforme ilustrado na figura, pela propriedade de soma de vetores, após obtermos a projeção ortogonal de na direção dada por (vetor em vermelho), podemos decompor em mais o vetor em azul, ou seja:
E conforme a nossa imagem sugere, o vetor em azul, que é exatamente aquele do qual fala a afirmação, é de fato perpendicular (ou ortogonal) a ! Podemos pensar da seguinte forma: quando subtraímos do vetor , o que estamos fazendo é efetivamente removendo de a parcela dele que existia na direção de , sobrando apenas o que é perpendicular a ela.
Passo 2
Para a afirmação (II), a única coisa que vamos precisar relembrar é da fórmula de projeção de um vetor na direção dada por um outro vetor :
Como nosso enunciado já nos deu que e , vamos substituir na fórmula:
Na fração temos que calcular dois produtos escalares. Mas como a base é ortonormal, só precisamos multiplicar as coordenadas e somar:
E tá pronto! Veja que obtemos direitinho o vetor que a afirmação (II) diz. Portanto, (II) é verdadeira.
Passo 3
Última afirmação, hein? Tá quase acabando. Para essa daqui, vamos primeiro dar uma relembrada no significado geométrico do determinante em termos de transformações lineares, beleza?
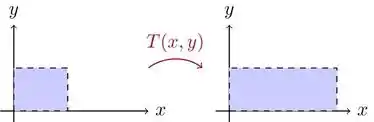
Em módulo, o determinante representa o quanto uma transformação expande ou contrai áreas ou volumes. Por exemplo, vamos considerar a transformação . Nas bases canônicas de , a matriz de T é dada por:
Se tirarmos o determinante, temos que . Mas de fato, essa transformação converte um quadrado de lado unitário em um retângulo de área , exatamente o mesmo fator de escala do determinante! Isso está ilustrado na figura abaixo.
Um outro exemplo que podemos dar é a rotação em , cuja matriz é dada em muitos cursos de Álgebra Linear como sendo:
Se tirarmos o determinante, temos: , pela identidade fundamental da trigonometria. E pelo nosso raciocínio até aqui, isso faz sentido, visto que numa rotação não há expansão ou contração de áreas, uma figura plana apenas giraria!
Beleza, mas e quanto ao sinal do determinante? Pois bem, o sinal está associado a uma mudança de orientação. Por exemplo, vamos considerar a transformação , cuja matriz nas bases canônicas do é dada por:
Tirando o determinante, temos . Uma ilustração de como age essa transformação está na figura abaixo:
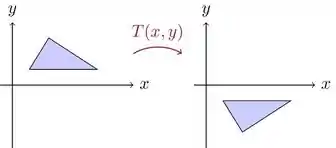
O triângulo à esquerda, que antes tinha a ponta apontando para cima, após a transformação tem sua ponta apontando para baixo. Se pensarmos em termos concretos, é como se pegássemos uma folha de papel na qual desenhamos um triângulo e então virássemos a folha do avesso. Não houve distorção das áreas, mas a orientação mudou!
Agora que fizemos essa nossa breve revisão, vamos tentar aplicá-la ao caso ! Na verdade, a lógica é a mesma. O sinal do determinante reflete a mudança de orientação. O foco aqui é a palavra mudança.
Pela nossa linha de raciocínio então, se sairmos de uma base negativa para uma base negativa de (ou de uma base positiva para uma base positiva), então não há mudança de orientação. Dessa forma, pela nossa lógica o determinante deveria ser positivo! E é mesmo hahah. Então já vimos que a alternativa é verdadeira.
Entendeu tudo direitinho? Valeu por chegar até aqui e vamos juntos para a próxima questão!
Resposta
(c) todas as afirmações são verdadeiras