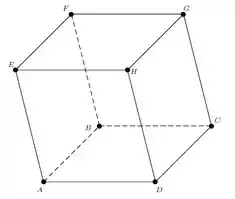
Considere os vetores , e no paralelepípedo da figura.
a) Justifique por que é uma base.
b) Determine as coordenadas do vetor na base .
c) Determine as coordenadas do vetor na base .
Passo 1
a) A gente viu lá na teoria que no , pra 3 vetores serem paralelos, eles devem ser paralelos ao mesmo plano.
Nesse caso, embora e sejam ambos paralelos ao plano da face , o vetor não é, logo, os 3 vetores não podem pertencer ao mesmo plano.
Então esses 3 vetores são L.I., e vimos que 3 vetores L.I. formam o que? Isso mesmoo, uma base :D
Passo 2
b) O que a gente tem que fazer aqui é escrever como combinação linear dos vetores da base . Sabemos que
Como e são congruentes assim como e , podemos escrever que
Estamos quase láá, agora você concorda que , é a mesma coisa que ? Então
Aee, agora temos o vetor escrito apenas em função de vetores da base
Passo 3
c) Esse passo é parecido com o anterior, temos que
Só precisamos mudar esse já que ele não pertence à base . Como e são congruentes:
Resposta
a) Demonstração.
b)
c)