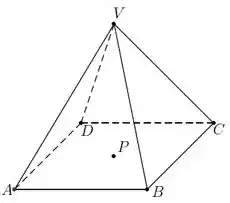
Em uma pirâmide regular tendo como base o quadrado e o vértice , considere a sequência de vetores e o ponto , projeção ortogonal do vértice na base da pirâmide.
a) Justifique por que é uma base.
b) Determine as coordenadas do vetor na base .
Passo 1
a) Pra que 3 vetores formem uma base eles devem ser L.I. certo? Beleza, e pra 3 vetores serem L.I., eles não podem ser coplanares.
Como é o vértice da pirâmide, ele não pode estar no mesmo plano da base, como a gente vê na imagem do enunciado. Assim, com certeza os vetores e não vão estar no mesmo plano, então eles são L.I. e é uma base :D
Passo 2
b) Vamo lá, a gente sabe que né?
Como é o ponto médio de , podemos escrever assim:
Como é congruente a e :
Então:
Conseguimos escrever o vetor em função dos vetores da base :D