UFRJ; Sem campus; Álgebra Linear 2; P2; 2022.2; Questão 7
Se , conjunto pode ser descrito como:
(A)
(B)
(C)
(D)
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin.Nosso objetivo é descobrir como
podemos descrever o conjunto . Onde
Bem o que seria ? Bem esse conjunto é a soma direta, e é definido como:
E como tem só o vetor nulo em sua interseção (os vetores são LI ), então
Será o espaço gerado pelos vetores
Como temos vetores isso gera um plano. Logo, nosso problema de identificar uma representação para virou o problema de identificar o plano gerado por
Passo 2
Agora, como podemos identificar os pontos de um plano? Para isso, usamos o vetor normal ao plano. Pois se um vetor qualquer pertence ao plano,então ele também será perpendicular ao vetor normal ao plano. Isso quer dizer que se for o vetor normal ao plano e se pertence ao plano, então
No nosso caso, qual é o vetor normal ao plano ?
Ora, é o vetor que perpendicular simultaneamente a , e podemos encontrar este vetor utilizando o produto vetorial entre .
Que é dado pelo determinante de
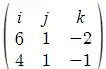
Que é:
Logo,
Passo 3
Como nosso vetor normal é dado por
Se então
Que é a equação do nosso plano.
Dessa forma, a alternativa correta é a letra
Se liguem, a equação só é essa pois o vetor nulo está contido em
Se o nosso plano fosse qualquer outro plano paralelo a esse, o vetor normal seria o mesmo, mas precisaríamos fazer uma correção na equação do plano. Para esse caso onde o plano é deslocado, temos que a equação é dada por:
Onde é um vetor pertencente ao plano.
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊