USP; Sem campus; Álgebra Linear 1; P1; 2022; Questão 7
Sejam e considere o sistema linear
nas incógnitas reais . Se esse sistema possui uma única solução, então
é igual a:
Assinale a alternativa correta:
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar quais as condições para que o sistema a seguir tenha uma única solução
e depois calcular
Bem, para um sistema ter uma única solução a primeira coisa que precisamos é ter o mesmo número de equações e variáveis livres. Vamos deixar essa informação guardada
Passo 2
Vamos começar escalonando a matriz que representa o nosso sistema aumentado ela é
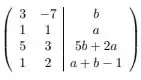
Vamos começar a escalonar esse sistema. Fazendo , temos:
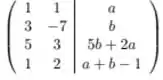
Agora, vamos fazer várias mudanças simultaneamente. Fazendo ; ; , e por último fazemos (trocamos de posição). Então temos:
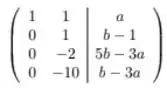
e, para finalizar, fazemos e . E obtemos
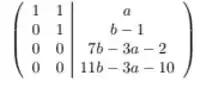
Prontinho, terminamos nosso escalonamento
Passo 3
Agora que temos nosso sistema aumentado escalonado. Podemos tentar verificar quando ele tem uma única solução
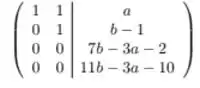
Bem, para ele ter solução, as duas últimas linhas da matriz aumentada precisam ser todas zeros. Pois, caso contrário, teremos um sistema impossível. Teremos algo da forma . Qur não tem solução. Logo precisamo que
subtraindo a primeira da segunda, temos
e
.
Logo, esse sistema só tem solução se
e
.
Passo 4
Ora mas se
e
.
Então
Valor presente na alternativa
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊