Considere a matriz

a entrada da matriz é:
(A)
(B)
(C)
(D)
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Essa é bem bacana, vamos trabalhar com inversão de matrizes. Lembram como fazemos isso? Para inverter uma matriz, precisamos resolver o sistema
Ou seja, precisamos resolver o sistema com a seguinte Matriz aumentada
E sua solução é a matriz . Lembraram como faz? Vamos a luta!
Passo 2
Como queremos a inversa de

Temos a seguinte matriz aumentada para resolver:
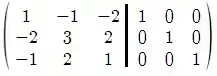
Vamos começar fazendo
e
Com isso, obtemos:
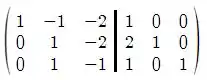
Fazemos
e
Com isso, obtemos:
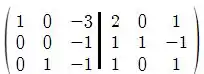
Fazemos:
e e
Com isso, obtemos:
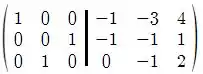
E, para finalizar, fazemos
Logo temos que o sistema escalonado é dado por
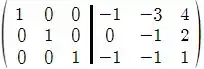
Então a matriz é:
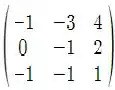
e
Dessa forma, a alternativa correta é a letra

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊