Os vetores u e v do formam as colunas da matriz A = [u|v]. Sabendo que
calcule .
(a) 1
(b) 5
(c) 0
(d) 2
Passo 1
Vamos pegar uma matriz genérica cuja transposta é e entender o que está acontecendo, nesse caso, estamos supondo que .
vai ser igual a :
Daí, tiramos que:
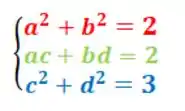
Até aí, ok?
A malandragem agora é olharmos para... Desenvolvendo para o e que supomos, teremos:
Identifica aí alguma coisa familiar?
Não?
Vamos organizar melhor...
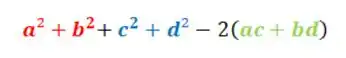
Agora ficou mais fácil, né?
Substituindo, teremos:
Resposta
Letra a
Exercícios de Livros Relacionados
36. Usando sua experiência com o exercício 35, projete um teste geral que possa ser aplicado a uma fórmula para aij para determinar se A=[a]ij é simétrica.
Se as entradas da matriz C = c 11 x c 21 x ⋮ c m 1 xc 12 x c 22 x ⋮ c m 2 x⋯ ⋯ ⋮ ⋯c 1 n x c 2 n x ⋮ c m n x São funções deriváveis de x , então definimos d C d x = c 11 ' x c 21 ' x ⋮ c m 1 ' xc 12 '
Se a b c d = m e a matriz de uma rotação em torno da origem, mostre que as colunas de m são vetores unitários ortogonais e o mesmo vale para as linhas.
Seja T:R ² →R ² ² ² a transformação linear que consiste em aplicar uma rotação de ângulo θ e depois trocar o sinal da segunda coordenada. Mostre que T é a reflexão em torno de uma reta r que contém a
Sejam r uma reta que contém a origem, α o ângulo de O X para reS :R ²→R ² ² ² a reflexão em torno de r . Sendo e 1=( 1 ,0 )ee 2=( 0 ,1 ) mostre que o ângulo de e 1 paraS e 1 é 2 α e o ângulo de e 2 pa