Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Operações com Matrizes

Ver Teoria
Exercício 541234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253555657

Enunciado

UFRJ; Sem campus; Álgebra Linear 2; P2; 2022.2; Questão 12

Considere R   :   R 2   →   R 2 uma reflexão em torno da reta gerada por s p a n   { ( − 4 ,   3 ) } . Seja ( a ,   b )   =   R ( 9 ,   12 ) .

Assinale o valor de a .

(A) 9

(B) - 9

(C) - 12

(D) 12 d d

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin.Nosso objetivo é encontrar o valor de a . Onde ( a ,   b )   =   R ( 9 ,   12 ) e R   :   R 2   →   R 2 uma reflexão em torno da reta gerada por s p a n   { ( − 4 ,   3 ) } .

Existe uma fórmula para calcularmos uma reflexão ao redor de uma reta que passa na origem. Lembram dela?

Ela é assim: Seja l = ( l x , l y ) o vetor paralelo à reta. Então a matriz de reflexão é dada por

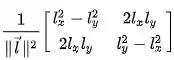
Vamos resolver a questão!

Passo 2

Bem, vamos começar encontrando nosso vetor paralelo a reta. Como nossa reta é gerada por s p a n   { ( − 4 ,   3 ) }

O vetor paralelo é:

( − 4 ,   3 )

Dessa forma, temos que

| l | 2 = 25

Então, a matriz de reflexão

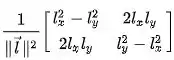
É

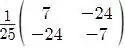
Como queremos encontrar a primeira coordenada da reflexão de ( 9 ,   12 ) , temos que

Log sua primeira entrada é o valor - 9

Dessa forma, a alternativa correta é a letra b )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

b )

Exercícios de Livros Relacionados

36. Usando sua experiência com o exercício 35, projete um teste geral que possa ser aplicado a uma fórmula para aij para determinar se A=[a]ij é simétrica.
Se as entradas da matriz C = c 11 x c 21 x ⋮ c m 1 xc 12 x c 22 x ⋮ c m 2 x⋯ ⋯ ⋮ ⋯c 1 n x c 2 n x ⋮ c m n x São funções deriváveis de x , então definimos d C d x = c 11 ' x c 21 ' x ⋮ c m 1 ' xc 12 '
Se a b c d = m e a matriz de uma rotação em torno da origem, mostre que as colunas de m são vetores unitários ortogonais e o mesmo vale para as linhas.
Seja T:R ² →R ² ² ² a transformação linear que consiste em aplicar uma rotação de ângulo θ e depois trocar o sinal da segunda coordenada. Mostre que T é a reflexão em torno de uma reta r que contém a
Sejam r uma reta que contém a origem, α o ângulo de O X para reS :R ²→R ² ² ² a reflexão em torno de r . Sendo e 1=( 1 ,0 )ee 2=( 0 ,1 ) mostre que o ângulo de e 1 paraS e 1 é 2 α e o ângulo de e 2 pa