A matriz que representa a reflexão através da reta em pode ser obtida pelo seguinte cálculo:
(Dica: será útil saber que o vetor é ortogonal à reta .)

Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nós queremos descobrir como calculamos a reflexão de um ponto através da reta . Mas como fazemos isso?

Bem, vamos pensar em como fazemos a reflexão em relação a reta . Nesse caso nós só invertemos o valor da coordenada do ponto. Ou seja
E a matriz que representa essa operação é:
![]()
Vamos guardar essa operação.
Passo 2
Bem, queremos a reflexão através da reta
Mas só sabemos fazer sob a reta . E agora? O que fazemos? Podemos pegar o ponto que queremos refletir em relação a reta , representar ele em uma base esperta. Que base seria essa?
Seria a base formada pelo próprio vetor diretor da reta e pelo vetor ortogonal a essa reta.
O vetor diretor da reta é é seu vetor ortogonal, informado no enunciado, é
Logo a matriz que faz a transformação
Logo a matriz de mudança para essa base esperta é
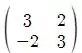
Logo, como podemos escrever a nossa reflexão? Bem, fazemos a mudança de base da canônica para a base esperta, aplicamos a matriz de projeção que vimos no passo e voltamos para a base canônica por meio da matriz inversa. Compondo essas matrizes obtemos:
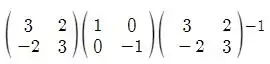
Que é igual a
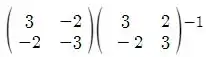
Matriz presente na alternativa

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊