USP; Sem campus; Álgebra Linear 1; P1; 2022; Questão 5
Sejam um inteiro, A uma matriz real e considere as afirmações abaixo.
(I) Seja a matriz obtida de trocando a primeira linha pela primeira coluna (mantendo inalteradas as entradas que não estão nem na primeira linha nem na primeira coluna). Vale que .
(II) Denote por a primeira, segunda e terceira linhas de , respectivamente. Se é a matriz obtida de trocando a primeira linha por , então , quaisquer que sejam .
(III) Se é uma matriz real qualquer e denota a transposta de uma matriz X, então
As afirmações verdadeiras são:
- apenas a 2 e 3
- apenas a 2
- apenas a 3
- apenas a 1 e 2
- apenas a 1 e 3
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez uma que usa as propriedades do determinante. Vamos fazer uma revisão sobre o determinante.
Temos que
e temos a seguinte propriedade
Se for somado, a uma linha (ou coluna) de , um múltiplo de outra linha (ou coluna) de , o determinante da nova matriz é igual ao de .
Passo 2
Bem, vamos começar verificando as nossas afirmações. A primeira diz que. Seja a matriz obtida de trocando a primeira linha pela primeira coluna (mantendo inalteradas as entradas que não estão nem na primeira linha nem na primeira coluna). Vale que .
E aí, como resolvemos isso? Ora, vamos dar um contra exemplo. Tome a matriz
Como duas de suas linhas são iguais. Seu determinante será zero. Em contrapartida, quando fazemos a troca da primeira linha com a primeira coluna, temos
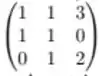
Que tem um determinante diferente de zero.
Logo, essa afirmação é falsa.
Passo 3
Vamos para a segunda afirmação. Denote por a primeira, segunda e terceira linhas de , respectivamente. Se é a matriz obtida de trocando a primeira linha por , então , quaisquer que sejam .
Bem, note que o que estamos fazendo aqui é substituir uma linha da matriz por ela mesma mais a combinação linear de outras linhas. Mas vimos na revisão que essa operação não altera o determinante. Logo essa afirmação é verdadeira.
Passo 4
Para finalizar, vamos checar a terceira afirmação. Que diz que se é uma matriz real qualquer e denota a transposta de uma matriz X, então
Como temos uma igualdade, podemos começar manipulando o lado esquerdo para tentar chegar no lado direito. Então usando que
Então a afirmação é correta. Portanto, chegamos a conclusão que as afirmações 2 e 3 são verdadeiras. Situação presente na alternativa
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊