Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Operações com Matrizes

Ver Teoria
Exercício 411234567891011121314151617181920212223242526272829303132333435363738394042434445464748495051525354555657

Enunciado

USP; Sem campus; Álgebra Linear 1; P1; 2022; Questão 14

Considere as matrizes

e seja A uma matriz real 2   ×   2 tal que ( X t A   −   Y   ) - 1 =   Z , em que X t denota a transposta da matriz X . Temos que o determinante de A é igual a:

  1. 7
  2.   5
  3. 3
  4. - 1
  5. - 5

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Essa é bem bacana, pois vamos trabalhar com manipulação de matrizes. Bem, queremos calcular o determinante da matriz A , mas sabemos que

( X t A   −   Y   ) - 1   =   Z

E

Como podemos fazer para calcular esse determinante? Ora, vamos descobrir qyem é a matriz A

Passo 2

Bem, como

( X t A   −   Y   ) - 1   =   Z

Então temos que

Z - 1 = X t A   −   Y

Logo

Z - 1 + Y = X t A

E por fim, temos que

( X - 1 ) t ( Z - 1 + Y ) = A

Logo, para descobrirmos que é A precisamos obter ( X - 1 ) e Z - 1

Passo 3

Como calculamos ( X - 1 ) e Z - 1 ? Poderíamos tentar resolver o sistema aumentado, mas como as matrizes são 2 x 2 podemos usar a fórmula

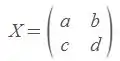
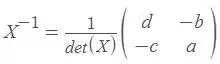
Dessa forma, como

Temos que

d e t ( X ) = 1 - 0

= 1

d e t ( Z ) = 1 - 0

= 1

Logo

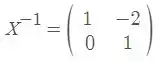
e

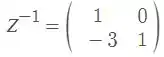
Passo 4

Agora que sabemos quem são

( X - 1 ) e Z - 1

Podemos calcular A

A = ( X - 1 ) t ( Z - 1 + Y )

Então temos:

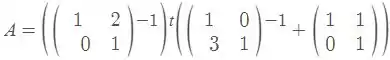
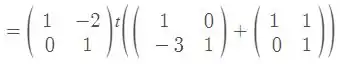
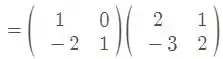
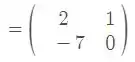
Logo, temos que o

d e t ( A ) = 2 * 0   -   1 ( - 7 )

= 7

Valor presente na alternativa a )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a )

Exercícios de Livros Relacionados

36. Usando sua experiência com o exercício 35, projete um teste geral que possa ser aplicado a uma fórmula para aij para determinar se A=[a]ij é simétrica.
Se as entradas da matriz C = c 11 x c 21 x ⋮ c m 1 xc 12 x c 22 x ⋮ c m 2 x⋯ ⋯ ⋮ ⋯c 1 n x c 2 n x ⋮ c m n x São funções deriváveis de x , então definimos d C d x = c 11 ' x c 21 ' x ⋮ c m 1 ' xc 12 '
Se a b c d = m e a matriz de uma rotação em torno da origem, mostre que as colunas de m são vetores unitários ortogonais e o mesmo vale para as linhas.
Seja T:R ² →R ² ² ² a transformação linear que consiste em aplicar uma rotação de ângulo θ e depois trocar o sinal da segunda coordenada. Mostre que T é a reflexão em torno de uma reta r que contém a
Sejam r uma reta que contém a origem, α o ângulo de O X para reS :R ²→R ² ² ² a reflexão em torno de r . Sendo e 1=( 1 ,0 )ee 2=( 0 ,1 ) mostre que o ângulo de e 1 paraS e 1 é 2 α e o ângulo de e 2 pa