Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Operações com Matrizes

Ver Teoria
Exercício 561234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545557

Enunciado

UFRJ; Sem campus; Álgebra Linear 2; P2; 2022.2; Questão 14

Sejam T ( x ,   y ,   z )   =   (   2   x   +   y   −   z ,   − 2   x   +   2   y   +   z   )   e   S ( x ,   y )   =   (   x   +   2   y ,   − 2   x   +   y ,   x   −   2   y   ) . Se A é a matriz que representa T   ◦   S , então sua entrada a 22 é:

(A) − 2

(B) − 4

(C) − 5

(D) − 3

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Uma sobre composição de transformações. Queremos descobrir quem é T   ◦   S . E para isso sabemos que

T ( x ,   y ,   z )   =   (   2   x   +   y   −   z ,   − 2   x   +   2   y   +   z   )  

S ( x ,   y )   =   (   x   +   2   y ,   − 2   x   +   y ,   x   −   2   y   )

E aí? Como fazemos essa composição? Ora, fazemos igual a composição de funções, vamos pegar a saída da transformação S e jogar na entrada transformação T

Passo 2

Bem, a saída da transformação S é

S ( x ,   y )   =   (   x   +   2   y ,   − 2   x   +   y ,   x   −   2   y   )

E da transformação T é

T ( x ' ,   y ' ,   z ' )   =   (   2   x '   +   y '   −   z ' ,   − 2   x '   +   2   y '   +   z '   )  

Logo,

T   ◦   S = T ( x   +   2   y ,   − 2   x   +   y ,   x   −   2   y )

= (   7 y - x ,       - 5 x - 4 y )

Agora que sabemos que

T   ◦   S ( x , y )     = (   7 y - x ,       - 5 x - 4 y )

Podemos verificar o que essa transformação faz com os vetores da base canônica de R 2

Passo 3

Sabendo que

T   ◦   S ( x , y )     = (   7 y - x ,       - 5 x - 4 y )

T   ◦   S ( 1,0 ) = ( - 1 , - 5 )

e

T   ◦   S ( 0,1 ) = ( 7 , - 4 )

Como sabemos o que a transformação faz com os elementos da base canônica, podemos expressar a matriz A da transformação como

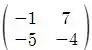
Dessa forma, a entrada a 22 é dada por - 4

logo a alternativa correta é a letra b )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

b )

Exercícios de Livros Relacionados

36. Usando sua experiência com o exercício 35, projete um teste geral que possa ser aplicado a uma fórmula para aij para determinar se A=[a]ij é simétrica.
Se as entradas da matriz C = c 11 x c 21 x ⋮ c m 1 xc 12 x c 22 x ⋮ c m 2 x⋯ ⋯ ⋮ ⋯c 1 n x c 2 n x ⋮ c m n x São funções deriváveis de x , então definimos d C d x = c 11 ' x c 21 ' x ⋮ c m 1 ' xc 12 '
Se a b c d = m e a matriz de uma rotação em torno da origem, mostre que as colunas de m são vetores unitários ortogonais e o mesmo vale para as linhas.
Seja T:R ² →R ² ² ² a transformação linear que consiste em aplicar uma rotação de ângulo θ e depois trocar o sinal da segunda coordenada. Mostre que T é a reflexão em torno de uma reta r que contém a
Sejam r uma reta que contém a origem, α o ângulo de O X para reS :R ²→R ² ² ² a reflexão em torno de r . Sendo e 1=( 1 ,0 )ee 2=( 0 ,1 ) mostre que o ângulo de e 1 paraS e 1 é 2 α e o ângulo de e 2 pa