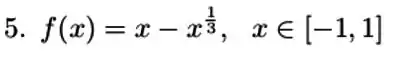
Passo 1
Para ver se a função satisfaz as hipóteses do teorema de Rolle temos que garantir que:
- A função seja contínua para todo o intervalo fechado .
- A função seja derivável para todo o intervalo aberto .
Passo 2
A função é uma função potência, que é contínua para todo . Assim, garantimos a primeira condição.
Passo 3
A derivada dessa função, segue a regra da derivação de funções potência, onde:
Essa derivada não vai existir para , pois teremos uma divisão por zero e .
Dessa maneira, o Teorema de Rolle não se aplica a essa função.
Resposta
Exercícios de Livros Relacionados
Sejaf x = tg x . Mostre que f 0 = f ( π ) , mas não existe um número c em ( 0 ,π ) tal que f ' c = 0 . Por que isso não contradiz o Teorema de Rolle?
Suponha que f seja uma função ímpar e derivável em toda a parte. Demonstre que para todo o número positivo b existe um número c em ( - b , b ) tal que f ' c = f b b .
Demonstre a identidade arcsen x - 1 x + 1 = 2 arctg x - π 2
Mostre que a equação 2 x - 1 - s e nx= 0 tem exatamente uma raiz real.
Dois corredores iniciam uma corrida no mesmo instante e terminam empatados. Demonstre que em algum momento durante a corrida, eles tinham a mesma velocidade. [Sugestão: Considere f t = g t - h ( t ) ,