ME01) Considere uma função derivável com e , e considere as afirmações abaixo:
- possui pelo menos uma raíz
- Para algum , vale que
- Para algum , vale que
Escolha a alternativa correta:
- Somente é verdadeira
- Somente é verdadeira
- Somente é verdadeira
- e são verdadeiras
- e são verdadeiras
- Todas são verdadeiras
- Todas são falsas
Passo 1
Vamos lá. Pra começar, note que sabemos pouquíssimo sobre a função. Na verdade, só sabemos dois pontos dela:
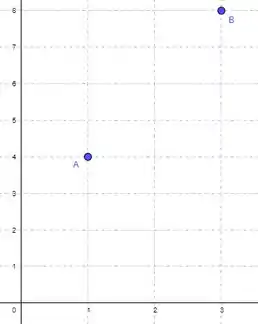
Mas veja bem, é derivável, logo ela tem que ser uma função contínua. Se ela é contínua, tem infinitas formas de desenharmos a função saindo de e indo até , mas todas as formas dão pra desenhar sem tirar a caneta do papel. Então, por exemplo, poderíamos desenhar assim:
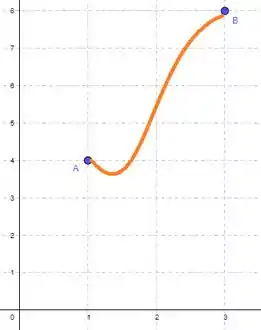
Agora, vamos ver as alternativas, beleza?
Passo 2
A letra diz que a função tem pelo menos uma raiz. Bem, nesse nosso primeiro esboço, em laranja, a função não tem. Mas ela bem poderia ter, né não? Nesse caso, poderíamos esboçar a curva bege também, que na verdade tem duas raízes:
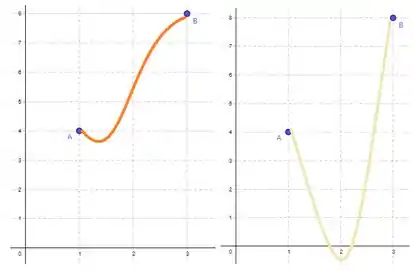
Ou a raiz poderia estar fora do intervalo , quem sabe? Bem, se não temos informações o suficiente pra provar que a função tem pelo menos uma raiz, é porque a afirmativa é falsa!
Passo 3
Bora pra afirmativa . Veja bem, ela diz que vai existir qualquer valor que faça com que seja igual à . Será que isso é verdade? Olhe bem os nossos dois primeiros esboços:
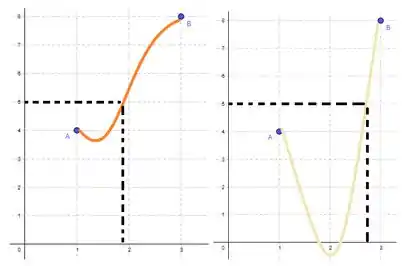
E veja só! Mesmo que a gente não saiba quem é o , nos dois esboços a curva passa por ! E isso cai exatamente no Teorema do Valor Intermediário. Já que é contínuo entre , vai existir pelo menos um tal que , uma vez que . Logo, verdadeiro!
Passo 4
E pra fechar, vamos analisar a afirmativa . Como ela fala de , o que ela esta dizendo é que a inclinação da reta tangente vai ser igual a em algum ponto entre e . Meio doido de pensar mas veja bem o que acontece se eu ligar os pontos e por uma reta:
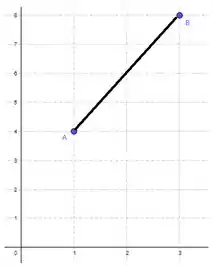
Eu posso pensar na inclinação dessa reta como sendo:
Opa, então essa reta tem inclinação ! Se eu transportar essa reta, com a mesma inclinação, para um ponto de tangência, aqueles dois esboços bem diferentes vão ter correspondência, saca só:
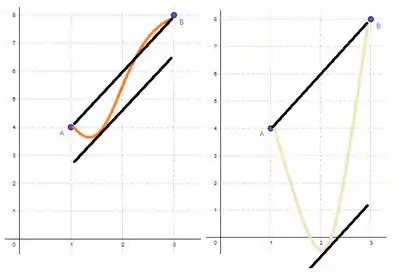
Eu não sei vocês mas eu acho isso lindo! As retas tangentes em um qualquer, igual à , mesmo que pra esboços diferentes (logo ’s diferentes), já que são paralelas a que traçamos inicialmente, tem sim inclinação ! E isso cai exatamente na definição de Teorema do Valor Médio:

Seja:
Temos então realmente:
Então a afirmativa e essa, a , estão corretas! Resposta final é a Letra