12) Seja uma função polinomial não constante.

a) Prove que, entre dois zeros consecutivos de (isto é, dois valores de que anulam a derivada e tal que entre eles não existe outro valor que anula a derivada), existe no máximo uma raiz de .

Ora! O problema fala de uma função polinomial qualquer e fala da sua derivada .

A derivada, geometricamente falando, representa o coeficiente da reta tangente. O que acontece quando a derivada tem um ? A reta tangente fica paralela ao eixo , certo? Então se a derivada tem dois zeros consecutivos, a reta tangente fica paralela ao eixo duas vezes, assim:

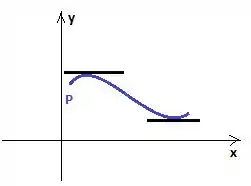
A curva em azul é a e a reta tangente em preto representa o fato da derivada se anular duas vezes consecutivo.

Note que no exemplo, a curva nem tem zero nenhum, mas ela poderia ter um zero:

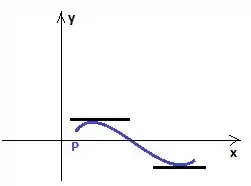
Mas zero é o máximo que poderia ter nessas condições, pois se ela tivesse duas ou mais, não estaria entre os pontos onde a derivada é consecultivamente:

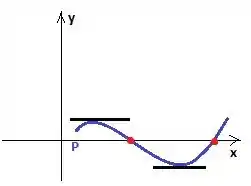
Sacou? Agora vamos provar isso matematicamente ;)

Vamos tentar uma prova que chamamos por absurdo. Vamos supor que de uma forma absurda, tem como da derivada zerar apenas duas vezes e a função ter mais de um zero no intervalo onde a derivada zerou.

Chamemos esse intervalo de ...

Vamos falar que o ponto que a curva zera, seja e (dois pontos de uma forma absurda)...

Onde esses pontos e , pertencem ao intervalo onde as derivadas se anulam...

Pelo Teorema de Rolle existe um dentro do intervalo que...

Como o intervalo pertence ao intervalo maior , existe um ponto do interior do intervalo que está zerando a derivada também. O que é um absurdo, pois nós falamos que a derivada só zera em e de uma forma consecutiva, saca?

Se existisse de fato esse , deixaria de ser consecutiva. Por isso só existe nó máximo uma raiz de nesse caso