Origem do Exercício
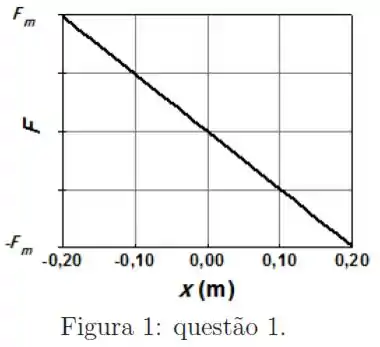
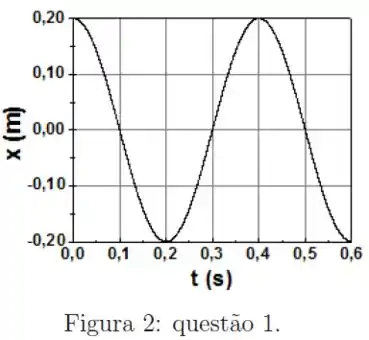
Um bloco de massa m está preso a uma parede através de uma mola de constante elástica k e sobre um piso horizontal sem atrito. A figura 1 mostra a força F que a mola exerce sobre o bloco em função da sua posição . Nesta figura, O bloco é deslocado até e depois liberado. A figura mostra a oscilação resultante em termos da posição em função do tempo .
a)Calcule o valor de .
b)Calcule o valor da velocidade máxima do bloco.
Passo 1
a)
Como a primeira figura relaciona a posição com a força, podemos usar a equação abaixo pra achar a constante da mola:
Assim, para
Da segunda figura, temos que:
Assim, usando:
Passo 2
b)
A gente pode usar a conservação da energia pra matar essa opção:
Para a velocidade máxima, temos energia cinética máxima, assim:
Da figura podemos tirar que a amplitude vale:
Assim:
Show?(:
Resposta
a)
b)