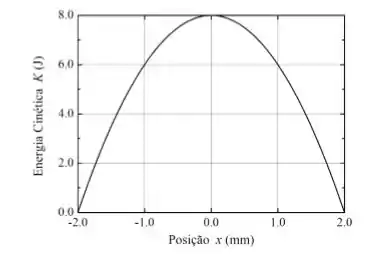
A figura abaixo mostra o gráfico da energia cinética de um sistema massa-mola em função da posição da massa. Determine o valor da constante elástica da mola em . Sabendo que o período de oscilação é s, encontre o valor da massa em . No instante , a massa encontra-se na posição com velocidade . Esboce o gráfico de sua posição para .
Passo 1
Para descobrirmos a constante elástica da mola, iremos usar a conservação de energia já que tudo que temos é um gráfico de energia cinética.
Nesse gráfico vemos a energia cinética, sair do zero, atingir um valor máximo em e depois cair até a energia ser zero novamente.
Como não há atuação de nenhuma força dissipativa, a energia mecânica se conserva, assim:
A energia mecânica é dada pela soma da energia potencial com a energia cinética
Sendo assim, podemos pelo gráfico calcular qual a energia mecânica quando
A energia potencial num sistema massa mola simples assim, é dada por
Como , então . Sendo assim:
A energia cinética o gráfico nos fornece, então
Agora voltando a conservação de energia mecânica, podemos escolher um momento qualquer do gráfico e descobrir qual é a energia potencia naquele momento. Para facilitar nossa vida, escolheremos , pois lá . Assim:
Lembrando que
Assim,
Passo 2
Precisamos lembrar de duas equações para resolvermos esse item:
E ainda que o período é o inverso da frequência. Assim, podemos igualar as equações e:
O período o problema deu, e a gente terminou de descobrir, assim só restou a massa:
Substituindo o período e
Passo 3
Para descrevermos o movimento da partícula em função do tempo a primeira coisa q temos q fazer é encontrar a equação do movimento.
Bem, sabemos que ela tem esse jeito:
A amplitude é fácil de encontrarmos, basta olharmos no gráfico da energia cinética e observamos quando a energia cinética é zero. Pois esse é o momento e máxima amplitude. Assim
A frequência natural é dada por
Assim,
Agora só precisamos descobrir a fase. O enunciado falou que em , a posição é , assim,
Então chegamos na equação do movimento em função do tempo e assim podemos construir o gráfico.
E o gráfico é assim:
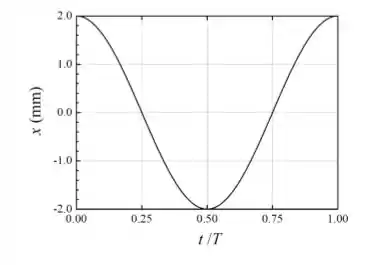
Para construir o gráfico você precisa marcar 5 pontos.
O primeiro é quando E o último é . Esses pontos terão a mesma altura, pois representa um período. Agora o 2º e 4º ponto serão quando
E o 3º ponto será quando . Ou seja, .
No nosso problema esses pontos são:
Marcando esses pontos, você traça a curva.
Resposta
/