Uma plataforma gira com velocidade constante em torno do eixo perpendicular ao seu centro. O referencial girante tem origem no centro da plataforma e gira com a mesma velocidade . Uma mola ideal de constante está presa na origem do referencial com uma massa presa a outra extremidade. A massa pode deslocar-se sem atrito apenas radialmente apenas no interior de duas guias laterais. Inicialmente a massa está presa por um pino de segurança à uma distância da origem e a mola encontra-se relaxada.
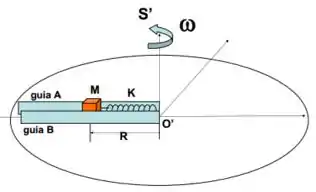
- Determine a posição de equilíbrio da massa a partir da posição inicial quando o pino de segurança for removido.
- Determine o vetor da força no referencial que a massa aplicará nas guias radiais quando passar pelo ponto de equilíbrio pela primeira vez.
- Qual será a força aplicada nas guias quando a massa atingir o seu deslocamento máximo?
Passo 1
a):
Beleza galera, pra acharmos essa posição, vamos ter que descobrir o que acontece de fato na posição de equilíbrio:
Nessa posição teremos o somatório de forças igual à zero, na direção radial, igual a zero.
E quais são as forças que agem na direção radial?
Tem a força peso e a força centrífuga, considerando-se o referencial não inercial girante que acompanha o sistema.
Então:
Quem é ?é a elongação da mola. Além disso, na força centrífuga nós usamos pois essa é a distância total que vai do centro do disso até a posição da partícula deslocada.
Como há equilíbrio, as forças precisam se anular e , portanto, serem iguais:
E esse é o valor da amplitude do movimento.
Mas em relação ao ponto , precisamos acrescentar o valor de
Lembrando que essa massa está realizando um MHS.
Passo 2
b):
A força que a amassa aplicará nas guias será a força de coriolis. Essa força é dada por:
Só precisamos descobrir , ou seja, a velocidade da massa na posição de equilíbrio.
Na posição de equilíbrio, a velocidade será máxima. Isso é, sendo a energia mecânica dada por:
Na posição de equilíbrio toda a energia mecânica será cinética:
Usando o valor de do item anterior:
Basta a gente substituir esse valor na fórmula. No entanto, precisamos determinar o sentido também.
Na primeira vez que passar pelo ponto de equilíbrio, a força será sobre a guia , pois a velocidade é para fora da plataforma, portanto sentido
Passo 3
c):
No deslocamento máximo não há velocidade, momentaneamente. É aquele ponto do MHS que a partícula muda de trajetória. Então, jogando na fórmula de coriolis
Resposta
a):
b):
c):