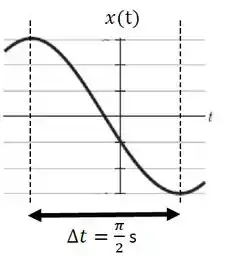
Um oscilador harmônico, composto de um bloco de massa e uma mola de constante elástica desconhecida, oscila de acordo com a função posição mostrada na figura. Considere que o oscilador é governado pela equação , com as grandezas no sistema internacional.
Determine:
(a) A frequência angular e a constante elástica da mola
(b) A constante de fase
(c) A(s) posição(ões) do bloco para que a energia potencial elástica seja metade da energia mecânica total
(d) O menor tempo para que o bloco vá da posição até o ponto de equilíbrio.
Passo 1
Pela figura vemos que o tempo entre um máximo e um mínimo, ou seja, meia volta, é . Como o período é o tempo em que a oscilação completa uma volta temos que
Passo 2
A massa se relaciona com a frequência angular por
Por outro lado, a frequência angular se relaciona com o período de oscilação por
Assim, temos que
Substituindo os valores
Passo 3
Sabemos, pelo enunciado, que
Se olharmos o gráfico, basta escolher um ponto e substituir. Eu acho que fica mais tranquilo escolher por que isso facilita um pouco as coisas. No gráfico temos que
A posição é , por que tem escalas em correspondendo à amplitude de oscilação que é .
Assim
Jogando na calculadora podemos ter dois resultados possíveis
Passo 4
Pra saber qual dos dois é o correto basta olhar a velocidade. Como
A velocidade vai ser dada por
Testando as duas possibilidades
Olhando o gráfico no tempo , vemos que a velocidade é negativa! Assim a opção que se ajusta pra essa velocidade será
Passo 5
A energia potencial do OHS é
Já a energia mecânica é dada por
A energia mecânica é constante, só fica alternando entre potencial e cinética. Quando a mola está totalmente esticada a velocidade é nula e a posição é a amplitude do movimento, ou seja
Como queremos que a energia potencial seja metade da energia mecânica basta fazer
Como a amplitude é
Passo 6
Vamos considerar que num tempo , o bloco esteja na posição e que num tempo esteja na origem, assim
Subtraindo as duas equações
Como
Resposta
(a)
(b)
(c)
(d)