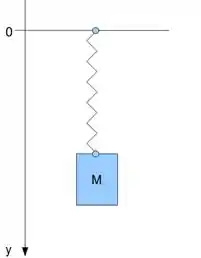
Uma massa M de é suspensa a uma mola de massa desprezível e constante elástica . A extremidade superior da mola é fixa. No repouso (sem a massa M) a mola tem comprimento.
- Qual é a posição da massa no equilíbrio?
- Sabendo que o período de oscilação pode ser aproximado pelo período de oscilação sem amortecimento, determinar o valor de ?
- Qual é a energia perdida durante as 5 oscilações?
No instante , a massa é afastada de da posição de equilíbrio e solta. A força de amortecimento é dada pela fórmula, onde é a velocidade da massa. Devido ao amortecimento, a amplitude cai da metade após 5 oscilações completas. No regime subcrítico, lembre-se de que a posição do objeto é dada por:
,
onde é a amplitude e é a constante de fase.
Passo 1
O sistema massa-mola estará em equilíbrio quando:
E como a mola relaxada tem comprimento de 50 cm, quando a massa estiver no equilíbrio a mola terá comprimento igual a 60 cm. Então, no equilíbrio:
Passo 2
Na letra b) temos que:
o período de oscilação pode ser aproximado pelo período de oscilação sem amortecimento, logo:
Agora vamos analisar o termo da equação abaixo, para obtermos o valor de :
,
temos que após 5 ciclos de oscilação esse termo fica na forma:
(
Passo 3
A energia perdida durante os 5 ciclos de oscilação, para pequenas perturbações, pode ser calculada de acordo com a expressão:
Em que:
,
Com:
Nós já temos todos os valores para poder aplicar na expressão. Vamos fazer primeiro para :
Então:
Resposta
a) 60 cm
b) 0,44 Kg/s
c) 1,5 J