O gráfico da Figura abaixo mostra a aceleração de uma partícula que executa um movimento harmônico simples. Seja a amplitude do movimento, pode-se dizer que:
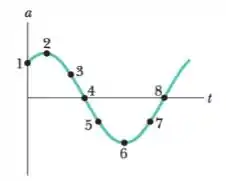
No ponto a partícula está na posição e no ponto a partícula está na posição
Nos pontos e a velocidade da partícula é nula.
No ponto a velocidade da partícula é negativa.
No ponto a partícula está na posição .
No ponto a partícula está entre e .
Passo 1
Antes de analisarmos o gráfico dado temos que lembrar as características de um HMS, temos que lembrar que na posição temos a máxima energia cinética. E nos pontos de máxima amplitude temos mínima energia cinética.
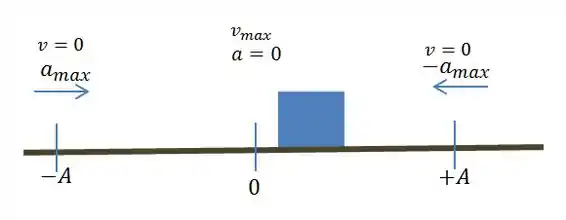
Agora podemos analisar o gráfico e as alternativas dadas.
A primeira diz que temos em . E em . O que é o contrário do que terminamos de ver. E faz sentido, porque se a aceleração fosse positiva em a partícula ia passar de .
Passo 2
A alternativa fala que quando a aceleração é zero, a velocidade também é nula. O que é muito errado se lembrarmos que a aceleração é a derivada da velocidade e temos derivada igual a zero quando a velocidade é máxima.
A alternativa diz que no ponto a velocidade é negativa. Já sabemos que ela era a máxima, agora para sabermos se é positiva ou negativa devemos olhar os sinais pouco antes e pouco depois. Pois se a aceleração está passando de positiva para negativa (que é o caso)
A velocidade vai ser positiva, pois o bloco está passando da região negativa, onde e indo para a região positiva onde .
A Alternativa contradiz tudo que que vimos nesse passo, pois vimos que quando a aceleração é nula, temos velocidade máxima e isso acontece em .
Passo 3
Ahh moleza, a alternativa correta é a , foi a única que sobrou né!
É verdade, mas vamos provar isso.
No ponto temos e isso mostra que estamos na posição . No ponto a aceleração é a máxima negativa e por isso temos que a posição nesse instante é .
Então no ponto a partícula está indo de para .
Resposta
Alternativa