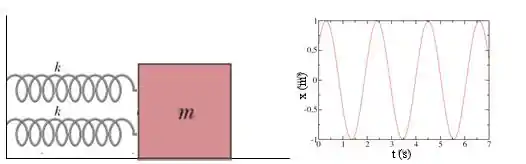
Considere o sistema abaixo formado por um bloco de massa e duas molas, cada uma de constante elástica . Este sistema está executando um movimento harmônico simples (MHS) cujo gráfico da posição como função do tempo também está ilustrado abaixo. Avalie como verdadeiras ou falsas as afirmações a seguir.
(I) Se na superfície da Terra, a frequência natural do sistema ´e , quando este é transportado para o espaço interestelar, a frequência ;
(II) Em , o sistema está se movendo com velocidade positiva e energia potencial diferente de zero;
(III) Como o sistema está executando um MHS, o período de oscilação é
(IV) Dado que no problema acima as molas estão associadas em paralelo, a frequência angular do MHS é
(V) Se a constante elástica de uma das molas fosse enquanto a da outra mola fosse , a frequência de oscilação do sistema seria o dobro.
(VI) Se agora há uma força dissipativa proporcional à velocidade se opondo ao movimento do sistema, as amplitudes de oscilação terão decaimento exponencial com o tempo e a frequência da oscilação será menor que a frequência de uma oscilação livre.
Passo 1
(I) Falsa: No MHS estamos desconsiderando qualquer força dissipativa. Portanto, estar na superfície da Terra ou no espaço leva à mesma frequência angular, pois em ambos os casos a energia mecânica do sistema é conservada e frequência angular só depende das características do sistema massa-mola;
(II) Verdadeira: A forma da curva de nos mostra que o sistema está se deslocando para a máxima amplitude, sendo assim, sua velocidade é positiva. Pela derivada da curva podemos também observar que a velocidade deve ser positiva;
(III) Falsa: Fazendo um diagrama de forças na situação em que a mola se encontra a uma distância x da posição de equilíbrio e aplicando a segunda lei de Newton, vemos que:
Deste modo, . Sabemos que o período é dado por:
(IV) Verdadeira: Pelo que vimos antes,.
(V) Falsa: Para duas molas de mesma constante elástica, vimos que .
Como
Para a situação onde , repetindo os passos em (III), chegamos a uma frequência angular: . Portanto:
(VI) Verdadeira: Vimos nos tópicos de ondas que:
Com
.
No caso deste problema, vemos que:
Resposta
(FVFVFV)