Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia no MHS

Ver Teoria
Exercício 30123456789101112131415161718192021222324252627282931323334353637383940414243444546474849505152535455565758596061626364656667686970

Enunciado

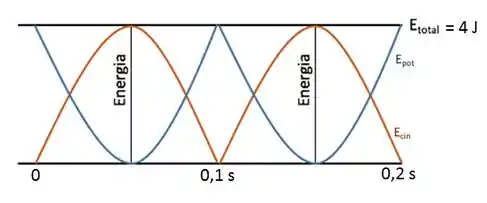
I – Um oscilador harmônico simples é formado por um bloco preso a uma mola com constante elástica k = 200 N/m. O bloco desliza em uma superfície sem atrito,com ponto de equilíbrio em x = 0. O gráfico da velocidade do bloco em função do tempo, v(t), aparece na figura.

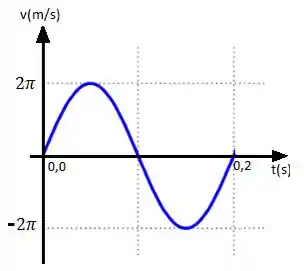
Considere: x t =   x m cos ⁡ ( ω t + φ )

Determine:

a) O período de oscilação do movimento, a frequência angular e a massa do bloco.

b) A amplitude do movimento.

c) A constante de fase e a função deslocamento x(t) do movimento.

d) A energia mecânica do oscilador.

e) O gráfico da energia cinética em função do tempo, indicando valores representativos das escalas (use o mesmo intervalo do gráfico acima).

Passo 1

a) A primeira coisa que a gente tem que ver é que ele deu o gráfico da velocidade! Nós não podemos fazer muita coisa com esse gráfico do jeito que ele ta aí. Mas ele também deu o modelo da posição em função do tempo:

x t =   x m cos ⁡ ( ω t + φ )

E você lembra que a velocidade é a derivada da posição? Então vamos derivar:

x ˙ t = - ω x m sin ⁡ ( ω t + φ )

Essa função sim nós podemos comparar com o gráfico! Então vamos lá. O período vai ser o mesmo nos dois gráficos. Olhando ali no gráfico da velocidade a gente consegue ver que:

T = 0,2   s

Que é o tempo que demora pro cara fazer uma oscilação completa.

A frequência angular a gente pode relacionar com o período usando a fórmula:

ω = 2 π T

Trocando então:

ω = 2 π 0,2

ω = 10 π   r a d / s

Por último nesse item ele pede a massa do bloco. No MHS, a frequência angular pode ser escrita com a massa e com o k da mola, assim:

ω 2 = k m

Como nós temos ω e k, é só substituir:

100 π 2 = 200 m

m = 2 π 2   k g

Passo 2

b) A amplitude do movimento vai ser o que tá multiplicando o cosseno. No caso,   x m . Nós podemos descobrir   x m comparando o gráfico com a função da velocidade. Assim:

x ˙ t = - ω x m sin ⁡ ( ω t + φ )

E a amplitude no gráfico é igual a 2 π . Então:

A = ω x m = 2 π

10 π x m = 2 π

x m = 0,2   m

Passo 3

c) Para achar φ vamos simplesmente fazer a velocidade para t = 0. Assim:

x ˙ t = - ω x m sin ⁡ ( ω t + φ )

x ˙ 0 = - ω x m sin ⁡ φ

Olhando lá no gráfico, x ˙ 0 = 0 . Então:

- ω x m sin ⁡ φ = 0

Pra isso rolar, φ tem que ser zero ou 180 ° (porque esses são os ângulos que têm seno zero). Então:

φ = 0

Ou:

φ = 180 °

Beleza, e agora? Qual dos dois usamos? Nós vamos olhar a derivada da velocidade:

x ¨ t = - ω 2 x m cos ⁡ ( ω t + φ )

Mas concorda comigo que, pelo gráfico da velocidade que ele deu, quando t = 0 teremos uma derivada positiva? Ou seja:

x ¨ 0 > 0

Para isso acontecer devemos ter φ = 180 ° :

x ¨ 0 = - ω 2 x m cos ⁡ φ

cos ⁡ φ < 0

Agora vamos substituir na posição:

x t =   x m cos ⁡ ( ω t + φ )

x t =   0,2 cos ⁡ ( 10 π t + π )

Passo 4

d) Bom, a energia mecânica total do sistema pode ser escrita:

E =   m v 2 2 + k x 2 2

Mas:

x t =   x m cos ⁡ ( ω t + φ )

v ( t ) = x ˙ t = - ω x m sin ⁡ ( ω t + φ )

Vamos substituir:

E =   m [ - ω x m sin ⁡ ( ω t + φ ) ] 2 2 + k [ x m cos ⁡ ω t + φ ] 2 2

E =   m ω 2 x m 2 sin 2 ⁡ ( ω t + φ ) 2 + k x m 2 cos 2 ⁡ ω t + φ 2

Vou trocar ω 2 por k/m:

E =   m k x m 2 sin 2 ⁡ ( ω t + φ ) 2 m + k x m 2 cos 2 ⁡ ω t + φ 2

E =   k x m 2 sin 2 ⁡ ( ω t + φ ) 2 + k x m 2 cos 2 ⁡ ω t + φ 2

E colocando em evidência:

E =   k x m 2 2 [ sin 2 ⁡ ω t + φ + cos 2 ⁡ ω t + φ ]

Olha que coisa bonita! Pela identidade trigonométrica podemos escrever:

sin 2 ⁡ ω t + φ + cos 2 ⁡ ω t + φ = 1

Então:

E =   k x m 2 2

Ou seja, a energia mecânica é constante! Substituindo os valores:

E =   200 ∙ ( 0,2 ) 2 2

E = 4   J

Passo 5

e) Nós já calculamos a energia cinética no item anterior, né. Vai ser:

E c i n é t i c a = m v 2 2 = m [ - ω x m sin ⁡ ( ω t + φ ) ] 2 2

E c i n é t i c a = k x m 2 sin 2 ⁡ ( ω t + φ ) 2

Substituindo aí os valores:

E c i n é t i c a = 200 ∙ ( 0,2 ) 2 sin 2 ⁡ ( ω t + φ ) 2

E c i n é t i c a = 4 sin 2 ⁡ ω t + φ

Lembrando que   φ = 180 ° !

E c i n é t i c a = 4 sin 2 ⁡ 10 π t + π

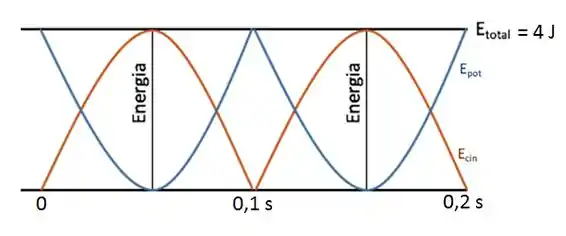
E o gráfico vai ficar:

Resposta

a) m = 2 π 2   k g

b) x m = 0,2   m

c) φ = 180 ° = π , x t =   x m cos ⁡ ( ω t + φ )

d) E = 4   J

e) E c i n é t i c a = 4 sin 2 ⁡ 10 π t + π

Exercícios de Livros Relacionados

Um furo de raio R / 4 é perfurado através de um cilindro de raio R para formar um corpo de massa m como mostrado. Se o corpo rola sobre a superfície horizontal sem deslizar, determine o período τ para
Um bloco de massa M = 5,4k g , em repouso em uma mesa horizontal sem atrito, está ligado a um suporte rígido através de uma mola de constante elástica k = 6000N / m . Uma bala de massa m = 9,5g e velo
Uma partícula de 10g executa um MHS com uma amplitude de 2,0m m , uma aceleração máxima de módulo 8,0.10 3 m / s 2 e uma constante de fase desconhecida φ . Qual é (a) o período do movimento, (b) a vel
Uma mola de massa desprezível está pendurada no teto com um pequeno objeto preso à extremidade inferior. O objeto é inicialmente mantido em repouso em uma posição y , tal que a mola se encontra no est
Um oscilador harmônico simples é formado por um bloco preso a uma mola com k = 200N / m . O bloco desliza em uma superfície sem atrito, com o ponto de equilíbrio em x = 0 e uma amplitude de 0,20m . O