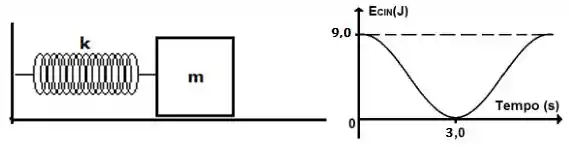
Um sistema massa-mola é colocado pra oscilar de modo que o gráfico abaixo mostra a energia cinética do bloco em função do tempo. Sabendo que a massa do sistema é M = 10Kg, qual é a amplitude do movimento em metros?
(a)
(b)
(c)
(d)
(e)
Passo 1
Bom, se já chegamos até aqui, já sabemos que um bloquinho como esse conectado a uma mola realiza um movimento harmônico simples (MHS).
Show de bola... E pelo princípio de conservação da energia mecânica, sabemos que a energia total mecânica (cinética + potencial) desse sistema é constante.
Mais um show de bola... E quando a mola está completamente esticada, sabemos que é máxima e é nula.
Olha o show de bola novamente... E quando a mola está completamente relaxada, é nula e é máxima.

![]() Show de bolas
Show de bolas
Looogo,
E a energia potencial:
Então:
Onde A é o deslocamento máximo, ou seja, amplitude que queremos determinar.
Passo 2
Do gráfico, :
Passo 3
Opa! Cancela o Show de bolas! Mas como podemos usar o k ali na fórmula???
Pode voltar com o Show de bolas... Nós vamos te dar o caminho...
Bom, do gráfico podemos determinaro período da onda, pois de um máximo até um mínimo de energia cinética temos um tempo de 3 segundos. Quando a mola está completamente esticada, temos um mínimo de energia cinética; quando ela passa pelo ponto de equilíbrio, temos um máximo de energia cinética. Isso corresponde a do movimento total... Então o período da onda será:
No MHS, temos que:
Substituindo na amplitude:
Como kg e :
Resposta
(b)