Um cilindro sólido de massa M = 4,0 kg está sobre uma superfície horizontal, preso pelo seu eixo a uma mola ideal horizontal de constante elástica k = 2,70 N/cm. O cilindro é afastado de 20,0 cm de sua posição de equilíbrio e abandonado a partir do repouso. Durante a oscilação o cilindro rola sem deslizar.
a) Mostre que o centro de massa do cilindro executa um movimento harmônico simples com período de .
b) Calcule as energias cinéticas de translação e de rotação do cilindro quando este passa pela posição de equilíbrio,
Passo 1
a) Vamos ver primeiro quais são as forças que atuam nesse cilindro. Dá uma olhada nessa figura:
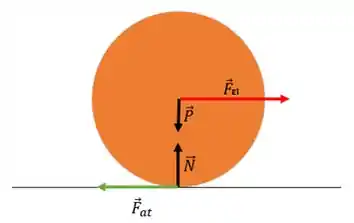
E essa força aí é a força elástica, ok?
Então escrevendo a segunda lei de Newton pra esse cara:
Guarde isso!
Passo 2
Beleza! Agora vamos escrever a segunda lei de Newton para rotações:
Em que R é o raio e o torque é negativo porque a força de atrito tá fazendo o cilindro girar no sentido horário. Além disso, só a força de atrito causa torque, porque a força elástica tá atuando no centro do cilindro.
Agora vamos trocar o que a gente tinha achado pra :
Guarde isso também!

Passo 3
Agora, tem duas coisas que você precisa saber. Primeiro, que a aceleração angular se relaciona com a aceleração linear dessa forma aqui:
Segundo, que a inércia I do cilindro é:
Então vamos trocar essas duas coisas na equação que achamos antes:
Comparando com a equação do MHS:
E o período vai ser:
Como queríamos demonstrar.

Passo 4
b) Aqui a gente precisa calcular as energias cinéticas de rotação e translação. Felizmente tem uma fórmula pra cada uma delas:
Lembrando que a velocidade linear se relaciona com a velocidade angular:
Vamos trocar I por e por :
E você concorda comigo que a soma dessas duas energias vai ser a energia cinética total? Então:
Passo 5
Ok, muita calma nessa hora.
Quando o cilindro (ou qualquer objeto em MHS) passa pelo equilíbrio, a velocidade dele é máxima! Então a energia cinética também vai ser máxima. Isso quer dizer que a energia cinética vai ser igual à energia mecânica (total) do sistema, que é constante.
Então, no equilíbrio:
Vamos trocar os valores que a gente conhece:
Passo 6
Maraviiiilha! Agora é só trocar nas energias de rotação e translação:
Resposta
a) Demonstração.

b) ,