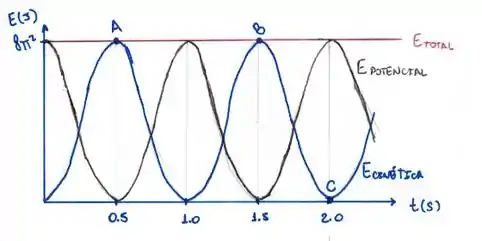
O gráfico mostra a energia cinética em função do tempo para um sistema massa-mola com . Considere que o sistema seja descrito pela equação
E que , o deslocamente
a) Esboce no mesmo gráfico a energia potencial da mola Represente também no mesmo gráfico a energia total do sistema massa-mola
Determine:
b) A constante de fase .
c) A frequência angular
d) A amplitude de movimento
e) A massa do bloco.
Passo 1
Onde a .
Passo 2
B)
Passo 3
C) Em A o corpo passa pela origem com v>0.
Em B o corpo passa pela origem com v
Em C o corpo retorna a posição inicial x(0).
Assim, pelo gráfico temos que t=2s
Passo 4
D)
Passo 5
E)
Logo
Resposta
A) Gráfico
B)
C)
D)
E)
Exercícios de Livros Relacionados
Um furo de raio R / 4 é perfurado através de um cilindro de raio R para formar um corpo de massa m como mostrado. Se o corpo rola sobre a superfície horizontal sem deslizar, determine o período τ para
Um bloco de massa M = 5,4k g , em repouso em uma mesa horizontal sem atrito, está ligado a um suporte rígido através de uma mola de constante elástica k = 6000N / m . Uma bala de massa m = 9,5g e velo
Uma partícula de 10g executa um MHS com uma amplitude de 2,0m m , uma aceleração máxima de módulo 8,0.10 3 m / s 2 e uma constante de fase desconhecida φ . Qual é (a) o período do movimento, (b) a vel
Uma mola de massa desprezível está pendurada no teto com um pequeno objeto preso à extremidade inferior. O objeto é inicialmente mantido em repouso em uma posição y , tal que a mola se encontra no est
Um oscilador harmônico simples é formado por um bloco preso a uma mola com k = 200N / m . O bloco desliza em uma superfície sem atrito, com o ponto de equilíbrio em x = 0 e uma amplitude de 0,20m . O