Seja um espaço vetorial e considere as seguintes afirmações:
- Se para todo inteiro existe um subconjunto linearmente independente de com elementos, então nenhum subconjunto finito de gera ;
- Se e são subespaços de tais que e se , são tais que
- Se e são subespaços de tais que é um subespaço de , então está contido em ou está contido em .
então e ;
Assinale a alternativa correta:
- apenas a afirmação (I) é necessariamente verdadeira;
- todas as afirmações são necessariamente verdadeiras;
- apenas as afirmações (I) e (III) são necessariamente verdadeiras;
- apenas as afirmações (I) e (II) são necessariamente verdadeiras;
- apenas as afirmações (II) e (III) são necessariamente verdadeiras.
Passo 1
Fala aí, gente!! Tudo bem? Vamos analisar cada uma das três afirmações, começando pela primeira, (I). Mas antes disso, vamos relembrar um pouco cada um dos conceitos que temos, para ficar bem claro. O que seria o tal conjunto gerador finito de que o enunciado fala?
A gente diz que um conjunto finito de vetores gera o espaço vetorial se qualquer vetor puder ser escrito como combinação linear deles, ou seja, se pudermos escrever algo da forma:
onde são os coeficientes da combinação linear.
Ora, mas vamos pensar o seguinte então: se um conjunto com elementos, como aquele nosso conjunto hipotético dali de cima consegue gerar qualquer vetor de , então nenhum conjunto com mais de elementos pode ser LI! Porque com certeza um ou mais deles vão ser combinação linear dos demais.
Com isso já matamos a charada da nossa questão, porque veja bem: se existisse algum conjunto gerador finito com elementos, então seria impossível para um inteiro que existisse um subconjunto linearmente independente de com elementos, conforme falamos ali em cima.
Assim, nossa primeira afirmação é verdadeira. Entendeu? 😊
Passo 2
Partindo para a segunda afirmação (II) temos a seguinte igualdade:
com e .
A nossa estratégia agora vai ser usar um truque bem simplesinho: vamos subtrair dos dois lados hahaha. Saca só:
Beleza. Eu só rearranjei a equação e você deve estar pensando “no que raios isso me ajuda?” Excelente pergunta! A diferença crucial entre essa equação rearranjada e a primeira é o seguinte: nos termos à direita e à esquerda do sinal de igual temos subtrações entre vetores que pertencem ao mesmo espaço vetorial!
Precisamos relembrar o seguinte: todo espaço vetorial é fechado por operações de soma e multiplicação por escalar. Então, como do lado esquerdo do temos que , então também é verdade que . A mesma coisa para , que implica .
Dessa forma, do lado esquerdo do temos um vetor pertencente a e do lado direito temos um vetor pertencente a .
Ora, mas o enunciado diz pra gente que , ou seja, o único vetor que pertence simultaneamente a e é o vetor nulo! Logo:
Então de fato concluímos que e e afirmação (II) é verdadeira.
Passo 3
Quase lá! Agora só falta a afirmação (III), hein? Se liga nessa figura que eu fiz aqui para gente:
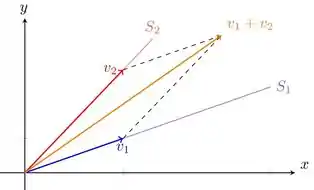
Aqui as duas retas que passam pela origem representam dois subespaços vetoriais do . Em cada uma delas, pegamos um vetor diferente, e . Note que a soma dos dois dá um vetor que não pertence a nenhum das duas retas!
Agora você deve estar se perguntando: “Beleza, mas para que serve isso?” Pois bem. Esse exemplo serve para ilustrar pra gente que a união de subespaços vetoriais no geral não é um subespaço vetorial!
Mas existe uma exceção, que é exatamente o caso que tá tratado nessa questão, se um deles estiver contido no outro, então a união dos dois dá o conjunto maior. Por exemplo, se , então . Como já é um subespaço vetorial, então a união também é!
O que a gente falou até aqui já deve ter dado pra perceber que a afirmação (III) é verdadeira, né? Hahah. Mas vamos tentar ir mais a fundo e provar isso.
Vamos supor que a conclusão da afirmação seja falsa e nem está contido em nem está contido em . Assim, existe algum vetor que pertence a , mas não a , ou seja, . Analogamente, existe algum vetor .
Show de bola, mas como é um subespaço de , então
Agora vamos usar nosso truquezinho de novo: subtrair haha. Fazendo isso, temos:
E de novo você deve estar pensando: “para que raios isso?!” Então, vamos em etapas: como , então ou .
- Se , como , então
- Se , como , então
Ora ora, mas em ambos os casos nós temos uma contradição, porque pertence a , mas não a , diferente do que concluímos. Analogamente, pertence a , mas não a . Só nos resta então concluir que nossa hipótese original estava errada, ou seja, é impossível que existam tal que e . Em outras palavras: ou está contido em ou está contido em .
Portanto, vemos que a afirmação (III) é mesmo verdadeira.
Ufa, acabamos!! Vamos para a próxima questão? 😊
Resposta
(b) todas as afirmações são necessariamente verdadeiras